Difference between revisions of "P-divisible group"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | p0710302.png | ||
| + | $#A+1 = 70 n = 3 | ||
| + | $#C+1 = 70 : ~/encyclopedia/old_files/data/P071/P.0701030 \BMI p\EMI\AAhdivisible group, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Barsotti–Tate group'' | ''Barsotti–Tate group'' | ||
| − | A generalization of the concept of a commutative [[Formal group|formal group]] of finite height. The homomorphism induced by multiplication by the prime number | + | A generalization of the concept of a commutative [[Formal group|formal group]] of finite height. The homomorphism induced by multiplication by the prime number $ p $ |
| + | is an epimorphism for a $ p $- | ||
| + | divisible group. | ||
| − | Let | + | Let $ S $ |
| + | be a [[Scheme|scheme]] and let $ p $ | ||
| + | be a prime number. A $ p $- | ||
| + | divisible group of height $ h $ | ||
| + | is an inductive system $ G = ( G _ {n} , i _ {n} ) $ | ||
| + | of commutative finite group schemes $ G _ {n} $ | ||
| + | of order $ p ^ {nh} $( | ||
| + | cf. [[Group scheme|Group scheme]]) such that the sequences | ||
| − | + | $$ | |
| + | 0 \rightarrow G _ {n} \rightarrow ^ { {i _ n} } G _ {n+} 1 \rightarrow ^ { {\phi _ n} } \ | ||
| + | G _ {n+} 1 | ||
| + | $$ | ||
| − | are exact (cf. [[Exact sequence|Exact sequence]]; here | + | are exact (cf. [[Exact sequence|Exact sequence]]; here $ \phi _ {n} $ |
| + | is the homomorphism of multiplication by $ p ^ {n} $). | ||
| + | A morphism of $ p $- | ||
| + | divisible groups is a morphism of the inductive systems. A $ p $- | ||
| + | divisible group is said to be connected (respectively, étale) if all $ G _ {n} $ | ||
| + | are connected (respectively, étale) group schemes. A connected $ p $- | ||
| + | divisible group over a field of characteristic $ p $ | ||
| + | is a commutative formal group (considered as the inductive limit of the kernels of $ \phi _ {n} $, | ||
| + | i.e. of multiplication by $ p ^ {n} $) | ||
| + | for which multiplication by $ p $ | ||
| + | is an [[Isogeny|isogeny]] [[#References|[6]]]. This fact is generalized to include the case of an arbitrary base scheme $ S $ | ||
| + | on which the homomorphism induced by multiplication by $ p $ | ||
| + | is locally nilpotent [[#References|[4]]]. The category of étale $ p $- | ||
| + | divisible groups is equivalent to the category of $ p $- | ||
| + | adic representations of the fundamental group of the scheme $ S $. | ||
| + | Each $ p $- | ||
| + | divisible group $ G $ | ||
| + | over an Artinian scheme $ S $ | ||
| + | contains a maximal connected subgroup $ G ^ {0} $, | ||
| + | which is known as the connected component of the identity, the quotient by which is an étale $ p $- | ||
| + | divisible group. The dimension of the Lie algebra of any $ {( G ^ {0} ) } _ {n} $ | ||
| + | is said to be the dimension of the $ p $- | ||
| + | divisible group $ G $. | ||
| − | Let | + | Let $ A $ |
| + | be an [[Abelian variety|Abelian variety]] over the field $ k $ | ||
| + | of dimension $ d $, | ||
| + | let $ A ( n) $ | ||
| + | be the kernel of the homomorphism of multiplication by $ p ^ {n} $ | ||
| + | in $ A $ | ||
| + | and let $ i _ {n} : A ( n) \rightarrow A ( n + 1 ) $ | ||
| + | be a natural inclusion. The inductive system $ A ( \infty ) = ( A ( n) , i _ {n} ) $ | ||
| + | is a $ p $- | ||
| + | divisible group of height $ 2d $. | ||
| + | Its connected component of the identity $ A ( \infty ) ^ {0} $ | ||
| + | coincides with the formal completion of $ A $ | ||
| + | along the unit section, while the height of $ A ( \infty ) ^ {0} $ | ||
| + | equals $ 2 \mathop{\rm dim} A $. | ||
| − | Let | + | Let $ G = ( G _ {n} , i _ {n} ) $ |
| + | be a $ p $- | ||
| + | divisible group of height $ h $, | ||
| + | let $ {\widehat{G} } _ {n} $ | ||
| + | denote the Cartier dual finite group schemes and let $ \widehat{i} _ {n} : \widehat{G} _ {n} \rightarrow \widehat{G} _ {n+} 1 $ | ||
| + | be the mapping dual to the mapping of multiplication by $ p : G _ {n+} 1 \rightarrow G _ {n} $. | ||
| + | The system $ \widehat{G} = ( \widehat{G} _ {n} , \widehat{i} _ {n} ) $ | ||
| + | is then a $ p $- | ||
| + | divisible group of height $ h $ | ||
| + | and is called the Serre dual to the $ p $- | ||
| + | divisible group $ G $. | ||
| + | The sum of the dimensions of $ G $ | ||
| + | and $ \widehat{G} $ | ||
| + | is equal to $ h $. | ||
| − | As in formal groups, so, too, in | + | As in formal groups, so, too, in $ p $- |
| + | divisible groups, the concept of a [[Dieudonné module|Dieudonné module]], which plays an important role in the deformation theory of $ p $- | ||
| + | divisible groups [[#References|[2]]], [[#References|[3]]], [[#References|[4]]] may be introduced. | ||
| − | If | + | If $ S $ |
| + | is the spectrum of an unequal-characteristic discrete valuation ring $ A $ | ||
| + | with residue field of characteristic $ p $, | ||
| + | the structure of a $ p $- | ||
| + | divisible group is closely connected with the structure of the completion of the algebraic closure of the quotient field $ K $ | ||
| + | of $ A $, | ||
| + | considered as a module over the Galois group of the field $ K $[[#References|[6]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I. Barsotti, "Analytic methods for abelian varieties in positive characteristic" , ''Coll. Théorie des Groupes Algébriques (Bruxelles, 1962)'' , Gauthier-Villars (1962) pp. 77–85</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Grothendieck, "Groupes de Barsotti–Tate et cristaux" , ''Proc. Internat. Congress Mathematicians (Nice, 1970)'' , '''1''' , Gauthier-Villars (1971) pp. 431–436</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B. Mazur, W. Messing, "Universal extensions and one-dimensional crystalline cohomology" , Springer (1974)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> W. Messing, "The crystals associated to Barsotti–Tate groups: with applications to Abelian schemes" , Springer (1972)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.-P. Serre, "Groupes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071030/p07103080.png" />-divisibles (d'après J. Tate)" , ''Sem. Bourbaki'' , '''318''' , Benjamin (1968)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J.T. Tate, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071030/p07103081.png" />-divisible groups" T.A. Springer (ed.) et al. (ed.) , ''Proc. Conf. local fields (Driebergen, 1966)'' , Springer (1967) pp. 158–183</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I. Barsotti, "Analytic methods for abelian varieties in positive characteristic" , ''Coll. Théorie des Groupes Algébriques (Bruxelles, 1962)'' , Gauthier-Villars (1962) pp. 77–85</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Grothendieck, "Groupes de Barsotti–Tate et cristaux" , ''Proc. Internat. Congress Mathematicians (Nice, 1970)'' , '''1''' , Gauthier-Villars (1971) pp. 431–436</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B. Mazur, W. Messing, "Universal extensions and one-dimensional crystalline cohomology" , Springer (1974)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> W. Messing, "The crystals associated to Barsotti–Tate groups: with applications to Abelian schemes" , Springer (1972)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.-P. Serre, "Groupes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071030/p07103080.png" />-divisibles (d'après J. Tate)" , ''Sem. Bourbaki'' , '''318''' , Benjamin (1968)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J.T. Tate, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071030/p07103081.png" />-divisible groups" T.A. Springer (ed.) et al. (ed.) , ''Proc. Conf. local fields (Driebergen, 1966)'' , Springer (1967) pp. 158–183</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Demazure, "Lectures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071030/p07103082.png" />-divisible groups" , ''Lect. notes in math.'' , '''302''' , Springer (1972)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Demazure, "Lectures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071030/p07103082.png" />-divisible groups" , ''Lect. notes in math.'' , '''302''' , Springer (1972)</TD></TR></table> | ||
Latest revision as of 08:04, 6 June 2020
Barsotti–Tate group
A generalization of the concept of a commutative formal group of finite height. The homomorphism induced by multiplication by the prime number $ p $ is an epimorphism for a $ p $- divisible group.
Let $ S $ be a scheme and let $ p $ be a prime number. A $ p $- divisible group of height $ h $ is an inductive system $ G = ( G _ {n} , i _ {n} ) $ of commutative finite group schemes $ G _ {n} $ of order $ p ^ {nh} $( cf. Group scheme) such that the sequences
$$ 0 \rightarrow G _ {n} \rightarrow ^ { {i _ n} } G _ {n+} 1 \rightarrow ^ { {\phi _ n} } \ G _ {n+} 1 $$
are exact (cf. Exact sequence; here $ \phi _ {n} $ is the homomorphism of multiplication by $ p ^ {n} $). A morphism of $ p $- divisible groups is a morphism of the inductive systems. A $ p $- divisible group is said to be connected (respectively, étale) if all $ G _ {n} $ are connected (respectively, étale) group schemes. A connected $ p $- divisible group over a field of characteristic $ p $ is a commutative formal group (considered as the inductive limit of the kernels of $ \phi _ {n} $, i.e. of multiplication by $ p ^ {n} $) for which multiplication by $ p $ is an isogeny [6]. This fact is generalized to include the case of an arbitrary base scheme $ S $ on which the homomorphism induced by multiplication by $ p $ is locally nilpotent [4]. The category of étale $ p $- divisible groups is equivalent to the category of $ p $- adic representations of the fundamental group of the scheme $ S $. Each $ p $- divisible group $ G $ over an Artinian scheme $ S $ contains a maximal connected subgroup $ G ^ {0} $, which is known as the connected component of the identity, the quotient by which is an étale $ p $- divisible group. The dimension of the Lie algebra of any $ {( G ^ {0} ) } _ {n} $ is said to be the dimension of the $ p $- divisible group $ G $.
Let $ A $ be an Abelian variety over the field $ k $ of dimension $ d $, let $ A ( n) $ be the kernel of the homomorphism of multiplication by $ p ^ {n} $ in $ A $ and let $ i _ {n} : A ( n) \rightarrow A ( n + 1 ) $ be a natural inclusion. The inductive system $ A ( \infty ) = ( A ( n) , i _ {n} ) $ is a $ p $- divisible group of height $ 2d $. Its connected component of the identity $ A ( \infty ) ^ {0} $ coincides with the formal completion of $ A $ along the unit section, while the height of $ A ( \infty ) ^ {0} $ equals $ 2 \mathop{\rm dim} A $.
Let $ G = ( G _ {n} , i _ {n} ) $ be a $ p $- divisible group of height $ h $, let $ {\widehat{G} } _ {n} $ denote the Cartier dual finite group schemes and let $ \widehat{i} _ {n} : \widehat{G} _ {n} \rightarrow \widehat{G} _ {n+} 1 $ be the mapping dual to the mapping of multiplication by $ p : G _ {n+} 1 \rightarrow G _ {n} $. The system $ \widehat{G} = ( \widehat{G} _ {n} , \widehat{i} _ {n} ) $ is then a $ p $- divisible group of height $ h $ and is called the Serre dual to the $ p $- divisible group $ G $. The sum of the dimensions of $ G $ and $ \widehat{G} $ is equal to $ h $.
As in formal groups, so, too, in $ p $- divisible groups, the concept of a Dieudonné module, which plays an important role in the deformation theory of $ p $- divisible groups [2], [3], [4] may be introduced.
If $ S $ is the spectrum of an unequal-characteristic discrete valuation ring $ A $ with residue field of characteristic $ p $, the structure of a $ p $- divisible group is closely connected with the structure of the completion of the algebraic closure of the quotient field $ K $ of $ A $, considered as a module over the Galois group of the field $ K $[6].
References
| [1] | I. Barsotti, "Analytic methods for abelian varieties in positive characteristic" , Coll. Théorie des Groupes Algébriques (Bruxelles, 1962) , Gauthier-Villars (1962) pp. 77–85 |
| [2] | A. Grothendieck, "Groupes de Barsotti–Tate et cristaux" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 431–436 |
| [3] | B. Mazur, W. Messing, "Universal extensions and one-dimensional crystalline cohomology" , Springer (1974) |
| [4] | W. Messing, "The crystals associated to Barsotti–Tate groups: with applications to Abelian schemes" , Springer (1972) |
| [5] | J.-P. Serre, "Groupes 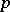 -divisibles (d'après J. Tate)" , Sem. Bourbaki , 318 , Benjamin (1968) -divisibles (d'après J. Tate)" , Sem. Bourbaki , 318 , Benjamin (1968) |
| [6] | J.T. Tate, "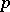 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 |
Comments
References
| [a1] | M. Demazure, "Lectures on 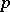 -divisible groups" , Lect. notes in math. , 302 , Springer (1972) -divisible groups" , Lect. notes in math. , 302 , Springer (1972) |
P-divisible group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P-divisible_group&oldid=13472