Outer measure

A non-negative set function, denoted by 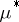, defined on a countably-additive class of sets that contains in addition to a set itself also any one of its subsets, and having the following properties:

monotony, i.e.

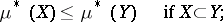countable semi-additivity, i.e.

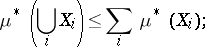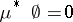, where 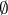is the empty set.

An outer measure defined on all subsets of a metric space is said to be an outer measure in the sense of Carathéodory, or a metric outer measure, if

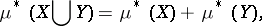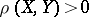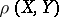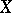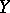provided that , where is the distance between the sets and . If an outer measure 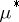is given, it is possible to specify the class of measurable sets on which 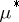becomes a measure (cf. also Carathéodory measure).

Outer measures result, in particular, from the construction of the extension of a measure from a ring 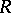onto the 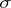-ring generated by it.

In the classical theory of the Lebesgue measure [1] the outer measure of a set is defined as the greatest lower bound of the measures of the open sets containing the given set; the inner measure of a set is defined as the least upper bound of the measures of the closed sets contained in the given set.

References

[1]	I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian)
[2]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)
[3]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)

References

[a1]	H.L. Royden, "Real analysis" , Macmillan (1968)