Ostrogradski method
A method for isolating the algebraic part in indefinite integrals of rational functions. Let  and
and  be polynomials with real coefficients, let the degree of
be polynomials with real coefficients, let the degree of  be less than the degree of
be less than the degree of  , so that
, so that  is a proper fraction, let
is a proper fraction, let
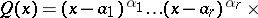 | (1) |
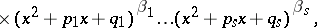 |
where  are real numbers,
are real numbers,  ,
, 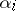 and
and  are natural numbers,
are natural numbers, 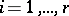 ,
, 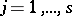 , and let
, and let
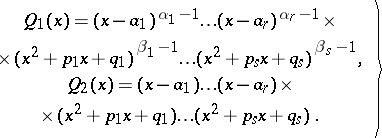 | (2) |
Then real polynomials 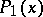 and
and 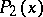 exist, the degrees of which are respectively less than the degrees
exist, the degrees of which are respectively less than the degrees 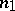 and
and  of the polynomials
of the polynomials 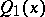 and
and  , such that
, such that
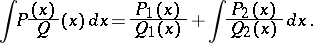 | (3) |
It is important that the polynomials  and
and  can be found without knowing the decomposition (1) of the polynomial
can be found without knowing the decomposition (1) of the polynomial  into irreducible factors: The polynomial
into irreducible factors: The polynomial 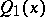 is the greatest common divisor of the polynomial
is the greatest common divisor of the polynomial 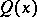 and its derivative
and its derivative 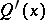 and can be obtained using the Euclidean algorithm, while
and can be obtained using the Euclidean algorithm, while  . The coefficients of the polynomials
. The coefficients of the polynomials  and
and 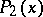 can be calculated using the method of indefinite coefficients (cf. Undetermined coefficients, method of). The Ostrogradski method reduces the problem of the integration of a real rational fraction to the integration of a rational fraction whose denominator has only simple roots; the integral of such a fraction is expressed through transcendental functions: logarithms and arctangents. Consequently, the rational fraction
can be calculated using the method of indefinite coefficients (cf. Undetermined coefficients, method of). The Ostrogradski method reduces the problem of the integration of a real rational fraction to the integration of a rational fraction whose denominator has only simple roots; the integral of such a fraction is expressed through transcendental functions: logarithms and arctangents. Consequently, the rational fraction  in formula (3) is the algebraic part of the indefinite integral
in formula (3) is the algebraic part of the indefinite integral 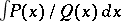 .
.
The method was first published in 1845 by M.V. Ostrogradski (see ).
References
| [1a] | M.V. Ostrogradski, Bull. Sci. Acad. Sci. St. Petersburg , 4 : 10–11 (1845) pp. 145–167 |
| [1b] | M.V. Ostrogradski, Bull. Sci. Acad. Sci. St. Petersburg , 4 : 18–19 (1845) pp. 286–300 |
Ostrogradski method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ostrogradski_method&oldid=48088