Osserman conjecture
Let  be the Riemann curvature tensor of a Riemannian manifold
be the Riemann curvature tensor of a Riemannian manifold  . Let
. Let  be the Jacobi operator. If
be the Jacobi operator. If  is a unit tangent vector at a point
is a unit tangent vector at a point  of
of  , then
, then  is a self-adjoint endomorphism of the tangent bundle at
is a self-adjoint endomorphism of the tangent bundle at  . If
. If  is flat or is locally a rank-
is flat or is locally a rank- symmetric space (cf. also Symmetric space), then the set of local isometries acts transitively on the sphere bundle
symmetric space (cf. also Symmetric space), then the set of local isometries acts transitively on the sphere bundle  of unit tangent vectors, so
of unit tangent vectors, so 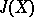 has constant eigenvalues on
has constant eigenvalues on  . R. Osserman [a6] wondered if the converse implication was valid; the following conjecture has become known as the Osserman conjecture: If
. R. Osserman [a6] wondered if the converse implication was valid; the following conjecture has become known as the Osserman conjecture: If  has constant eigenvalues, then
has constant eigenvalues, then  is flat or is locally a rank-
is flat or is locally a rank- symmetric space.
symmetric space.
Let  be the dimension of
be the dimension of  . If
. If  is odd, if
is odd, if  modulo
modulo  , or if
, or if  , then C.S. Chi [a3] has established this conjecture using a blend of tools from algebraic topology and differential geometry. There is a corresponding purely algebraic problem. Let
, then C.S. Chi [a3] has established this conjecture using a blend of tools from algebraic topology and differential geometry. There is a corresponding purely algebraic problem. Let  be a
be a  -tensor on
-tensor on  which defines a corresponding curvature operator
which defines a corresponding curvature operator  . If
. If 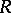 satisfies the identities,
satisfies the identities,
 |
 |
then  is said to be an algebraic curvature tensor. The Riemann curvature tensor of a Riemannian metric is an algebraic curvature tensor. Conversely, given an algebraic curvature tensor at a point
is said to be an algebraic curvature tensor. The Riemann curvature tensor of a Riemannian metric is an algebraic curvature tensor. Conversely, given an algebraic curvature tensor at a point  of
of  , there always exists a Riemannian metric whose curvature tensor at
, there always exists a Riemannian metric whose curvature tensor at  is
is  . Let
. Let  ; this is a self-adjoint endomorphism of the tangent bundle at
; this is a self-adjoint endomorphism of the tangent bundle at  . One says that
. One says that  is Osserman if the eigenvalues of
is Osserman if the eigenvalues of  are constant on the unit sphere
are constant on the unit sphere  in
in  . C.S. Chi classified the Osserman algebraic curvature tensors for
. C.S. Chi classified the Osserman algebraic curvature tensors for 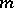 odd or
odd or  modulo
modulo  ; he then used the second Bianchi identity to complete the proof. However, if
; he then used the second Bianchi identity to complete the proof. However, if  modulo
modulo  , it is known [a4] that there are Osserman algebraic curvature tensors which are not the curvature tensors of rank-
, it is known [a4] that there are Osserman algebraic curvature tensors which are not the curvature tensors of rank-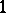 symmetric spaces and the classification promises to be considerably more complicated in these dimensions.
symmetric spaces and the classification promises to be considerably more complicated in these dimensions.
There is a generalization of this conjecture to metrics of higher signature. In the Lorentzian setting, one can show that any algebraic curvature tensor which is Osserman is the algebraic curvature tensor of a metric of constant sectional curvature; it then follows that any Osserman Lorentzian metric has constant sectional curvature [a2]. For metrics of higher signature, the Jordan normal form of the Jacobi operator enters; the Jacobi operator need not be diagonalizable. There exist indefinite metrics which are not locally homogeneous, so that  is nilpotent for all tangent vectors
is nilpotent for all tangent vectors  , see, for example, [a5].
, see, for example, [a5].
If  is an orthonormal basis for an
is an orthonormal basis for an  -plane
-plane  , one can define a higher-order Jacobi operator
, one can define a higher-order Jacobi operator
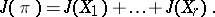 |
One says that an algebraic curvature tensor or Riemannian metric is  -Osserman if the eigenvalues of
-Osserman if the eigenvalues of  are constant on the Grassmannian of non-oriented
are constant on the Grassmannian of non-oriented  -planes in the tangent bundle. I. Stavrov [a8] and G. Stanilov and V. Videv [a7] have obtained some results in this setting.
-planes in the tangent bundle. I. Stavrov [a8] and G. Stanilov and V. Videv [a7] have obtained some results in this setting.
In the Riemannian setting, if  I. Dotti, M. Druetta and P. Gilkey [a1] have recently classified the
I. Dotti, M. Druetta and P. Gilkey [a1] have recently classified the  -Osserman algebraic curvature tensors and showed that the only
-Osserman algebraic curvature tensors and showed that the only  -Osserman metrics are the metrics of constant sectional curvature.
-Osserman metrics are the metrics of constant sectional curvature.
References
| [a1] | I. Dotti, M. Druetta, P. Gilkey, "Algebraic curvature tensors which are  Osserman" Preprint (1999) Osserman" Preprint (1999) |
| [a2] | N. Blažić, N. Bokan, P. Gilkey, "A note on Osserman Lorentzian manifolds" Bull. London Math. Soc. , 29 (1997) pp. 227–230 |
| [a3] | C.S. Chi, "A curvature characterization of certain locally rank one symmetric spaces" J. Diff. Geom. , 28 (1988) pp. 187–202 |
| [a4] | P. Gilkey, "Manifolds whose curvature operator has constant eigenvalues at the basepoint" J. Geom. Anal. , 4 (1994) pp. 155–158 |
| [a5] | E. Garcia-Rio, D.N. Kupeli, M.E. Vázquez-Abal, "On a problem of Osserman in Lorentzian geometry" Diff. Geom. Appl. , 7 (1997) pp. 85–100 |
| [a6] | R. Osserman, "Curvature in the eighties" Amer. Math. Monthly , 97 (1990) pp. 731–756 |
| [a7] | G. Stanilov, V. Videv, "Four dimensional pointwise Osserman manifolds" Abh. Math. Sem. Univ. Hamburg , 68 (1998) pp. 1–6 |
| [a8] | I. Stavrov, "A note on generalized Osserman manifolds" Preprint (1998) |
Osserman conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osserman_conjecture&oldid=15029