Difference between revisions of "Osserman conjecture"
(Importing text file) |
m (texified) |
||
| Line 1: | Line 1: | ||
| − | Let | + | Let $R$ be the Riemann [[Curvature tensor|curvature tensor]] of a [[Riemannian manifold|Riemannian manifold]] $(M,g)$. Let $J(X):Y\to R(Y,X)X)$ be the Jacobi operator. If $X$ is a unit tangent vector at a point $P$ of $M$, then $J(X)$ is a self-adjoint endomorphism of the [[Tangent bundle|tangent bundle]] at $P$. If $(M,g)$ is flat or is locally a rank-$1$ symmetric space (cf. also [[Symmetric space|Symmetric space]]), then the set of local isometries acts transitively on the sphere bundle $S(TM)$ of unit tangent vectors, so $J(X)$ has constant eigenvalues on $S(TM)$. R. Osserman [[#References|[a6]]] wondered if the converse implication was valid; the following conjecture has become known as the Osserman conjecture: If $J(X)$ has constant eigenvalues, then $(M,g)$ is flat or is locally a rank-$1$ symmetric space. |
| − | Let | + | Let $m$ be the dimension of $M$. If $m$ is odd, if $m\equiv2$ modulo $4$, or if $m=4$, then C.S. Chi [[#References|[a3]]] has established this conjecture using a blend of tools from [[Algebraic topology|algebraic topology]] and [[Differential geometry|differential geometry]]. There is a corresponding purely algebraic problem. Let $R(X,Y,Z,W)$ be a $4$-tensor on $R^m$ which defines a corresponding curvature operator $R(X,Y)$. If $R$ satisfies the identities, |
| − | + | \begin{equation}R(X,Y)=-R(Y,X),\\g(R(X,Y)Z,W)=g(R(Z,W)X,Y),R(X,Y)Z+R(Y,Z)X+R(Z,X)Y=0,\end{equation} | |
| − | + | then $R$ is said to be an algebraic curvature tensor. The Riemann curvature tensor of a Riemannian metric is an algebraic curvature tensor. Conversely, given an algebraic curvature tensor at a point $P$ of $M$, there always exists a Riemannian metric whose curvature tensor at $P$ is $R$. Let $J(X):Y\to R(Y,X)X$; this is a self-adjoint endomorphism of the tangent bundle at $P$. One says that $R$ is Osserman if the eigenvalues of $J(X)$ are constant on the unit sphere $S^{m-1}$ in $R^m$. C.S. Chi classified the Osserman algebraic curvature tensors for $m$ odd or $m\equiv 2$ modulo $4$; he then used the second [[Bianchi identity|Bianchi identity]] to complete the proof. However, if $m\equiv 0$ modulo $4$, it is known [[#References|[a4]]] that there are Osserman algebraic curvature tensors which are not the curvature tensors of rank-$1$ symmetric spaces and the classification promises to be considerably more complicated in these dimensions. | |
| − | + | There is a generalization of this conjecture to metrics of higher signature. In the Lorentzian setting, one can show that any algebraic curvature tensor which is Osserman is the algebraic curvature tensor of a metric of constant sectional curvature; it then follows that any Osserman Lorentzian metric has constant sectional curvature [[#References|[a2]]]. For metrics of higher signature, the Jordan normal form of the Jacobi operator enters; the Jacobi operator need not be diagonalizable. There exist indefinite metrics which are not locally homogeneous, so that $J(X)$ is nilpotent for all tangent vectors $X$, see, for example, [[#References|[a5]]]. | |
| − | + | If $\{X_1,...,X_r\}$ is an orthonormal basis for an $r$-plane $\pi$, one can define a higher-order Jacobi operator | |
| − | + | \begin{equation}J(\pi)=J(X_1)+...+J(X_r).\end{equation} | |
| − | + | One says that an algebraic curvature tensor or Riemannian metric is $r$-Osserman if the eigenvalues of $J(\pi)$ are constant on the Grassmannian of non-oriented $r$-planes in the tangent bundle. I. Stavrov [[#References|[a8]]] and G. Stanilov and V. Videv [[#References|[a7]]] have obtained some results in this setting. | |
| − | + | In the Riemannian setting, if $2\leq r\leq m-2$ I. Dotti, M. Druetta and P. Gilkey [[#References|[a1]]] have recently classified the $r$-Osserman algebraic curvature tensors and showed that the only $r$-Osserman metrics are the metrics of constant sectional curvature. | |
| − | |||
| − | In the Riemannian setting, if | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I. Dotti, M. Druetta, P. Gilkey, "Algebraic curvature tensors which are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o120/o120090/o12009061.png" /> Osserman" ''Preprint'' (1999)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Blažić, N. Bokan, P. Gilkey, "A note on Osserman Lorentzian manifolds" ''Bull. London Math. Soc.'' , '''29''' (1997) pp. 227–230</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C.S. Chi, "A curvature characterization of certain locally rank one symmetric spaces" ''J. Diff. Geom.'' , '''28''' (1988) pp. 187–202</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Gilkey, "Manifolds whose curvature operator has constant eigenvalues at the basepoint" ''J. Geom. Anal.'' , '''4''' (1994) pp. 155–158</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> E. Garcia-Rio, D.N. Kupeli, M.E. Vázquez-Abal, "On a problem of Osserman in Lorentzian geometry" ''Diff. Geom. Appl.'' , '''7''' (1997) pp. 85–100</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Osserman, "Curvature in the eighties" ''Amer. Math. Monthly'' , '''97''' (1990) pp. 731–756</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> G. Stanilov, V. Videv, "Four dimensional pointwise Osserman manifolds" ''Abh. Math. Sem. Univ. Hamburg'' , '''68''' (1998) pp. 1–6</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> I. Stavrov, "A note on generalized Osserman manifolds" ''Preprint'' (1998)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I. Dotti, M. Druetta, P. Gilkey, "Algebraic curvature tensors which are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o120/o120090/o12009061.png" /> Osserman" ''Preprint'' (1999)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Blažić, N. Bokan, P. Gilkey, "A note on Osserman Lorentzian manifolds" ''Bull. London Math. Soc.'' , '''29''' (1997) pp. 227–230</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C.S. Chi, "A curvature characterization of certain locally rank one symmetric spaces" ''J. Diff. Geom.'' , '''28''' (1988) pp. 187–202</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Gilkey, "Manifolds whose curvature operator has constant eigenvalues at the basepoint" ''J. Geom. Anal.'' , '''4''' (1994) pp. 155–158</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> E. Garcia-Rio, D.N. Kupeli, M.E. Vázquez-Abal, "On a problem of Osserman in Lorentzian geometry" ''Diff. Geom. Appl.'' , '''7''' (1997) pp. 85–100</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Osserman, "Curvature in the eighties" ''Amer. Math. Monthly'' , '''97''' (1990) pp. 731–756</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> G. Stanilov, V. Videv, "Four dimensional pointwise Osserman manifolds" ''Abh. Math. Sem. Univ. Hamburg'' , '''68''' (1998) pp. 1–6</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> I. Stavrov, "A note on generalized Osserman manifolds" ''Preprint'' (1998)</TD></TR></table> | ||
Latest revision as of 18:06, 5 February 2021
Let $R$ be the Riemann curvature tensor of a Riemannian manifold $(M,g)$. Let $J(X):Y\to R(Y,X)X)$ be the Jacobi operator. If $X$ is a unit tangent vector at a point $P$ of $M$, then $J(X)$ is a self-adjoint endomorphism of the tangent bundle at $P$. If $(M,g)$ is flat or is locally a rank-$1$ symmetric space (cf. also Symmetric space), then the set of local isometries acts transitively on the sphere bundle $S(TM)$ of unit tangent vectors, so $J(X)$ has constant eigenvalues on $S(TM)$. R. Osserman [a6] wondered if the converse implication was valid; the following conjecture has become known as the Osserman conjecture: If $J(X)$ has constant eigenvalues, then $(M,g)$ is flat or is locally a rank-$1$ symmetric space.
Let $m$ be the dimension of $M$. If $m$ is odd, if $m\equiv2$ modulo $4$, or if $m=4$, then C.S. Chi [a3] has established this conjecture using a blend of tools from algebraic topology and differential geometry. There is a corresponding purely algebraic problem. Let $R(X,Y,Z,W)$ be a $4$-tensor on $R^m$ which defines a corresponding curvature operator $R(X,Y)$. If $R$ satisfies the identities,
\begin{equation}R(X,Y)=-R(Y,X),\\g(R(X,Y)Z,W)=g(R(Z,W)X,Y),R(X,Y)Z+R(Y,Z)X+R(Z,X)Y=0,\end{equation}
then $R$ is said to be an algebraic curvature tensor. The Riemann curvature tensor of a Riemannian metric is an algebraic curvature tensor. Conversely, given an algebraic curvature tensor at a point $P$ of $M$, there always exists a Riemannian metric whose curvature tensor at $P$ is $R$. Let $J(X):Y\to R(Y,X)X$; this is a self-adjoint endomorphism of the tangent bundle at $P$. One says that $R$ is Osserman if the eigenvalues of $J(X)$ are constant on the unit sphere $S^{m-1}$ in $R^m$. C.S. Chi classified the Osserman algebraic curvature tensors for $m$ odd or $m\equiv 2$ modulo $4$; he then used the second Bianchi identity to complete the proof. However, if $m\equiv 0$ modulo $4$, it is known [a4] that there are Osserman algebraic curvature tensors which are not the curvature tensors of rank-$1$ symmetric spaces and the classification promises to be considerably more complicated in these dimensions.
There is a generalization of this conjecture to metrics of higher signature. In the Lorentzian setting, one can show that any algebraic curvature tensor which is Osserman is the algebraic curvature tensor of a metric of constant sectional curvature; it then follows that any Osserman Lorentzian metric has constant sectional curvature [a2]. For metrics of higher signature, the Jordan normal form of the Jacobi operator enters; the Jacobi operator need not be diagonalizable. There exist indefinite metrics which are not locally homogeneous, so that $J(X)$ is nilpotent for all tangent vectors $X$, see, for example, [a5].
If $\{X_1,...,X_r\}$ is an orthonormal basis for an $r$-plane $\pi$, one can define a higher-order Jacobi operator
\begin{equation}J(\pi)=J(X_1)+...+J(X_r).\end{equation}
One says that an algebraic curvature tensor or Riemannian metric is $r$-Osserman if the eigenvalues of $J(\pi)$ are constant on the Grassmannian of non-oriented $r$-planes in the tangent bundle. I. Stavrov [a8] and G. Stanilov and V. Videv [a7] have obtained some results in this setting.
In the Riemannian setting, if $2\leq r\leq m-2$ I. Dotti, M. Druetta and P. Gilkey [a1] have recently classified the $r$-Osserman algebraic curvature tensors and showed that the only $r$-Osserman metrics are the metrics of constant sectional curvature.
References
| [a1] | I. Dotti, M. Druetta, P. Gilkey, "Algebraic curvature tensors which are 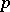 Osserman" Preprint (1999) Osserman" Preprint (1999) |
| [a2] | N. Blažić, N. Bokan, P. Gilkey, "A note on Osserman Lorentzian manifolds" Bull. London Math. Soc. , 29 (1997) pp. 227–230 |
| [a3] | C.S. Chi, "A curvature characterization of certain locally rank one symmetric spaces" J. Diff. Geom. , 28 (1988) pp. 187–202 |
| [a4] | P. Gilkey, "Manifolds whose curvature operator has constant eigenvalues at the basepoint" J. Geom. Anal. , 4 (1994) pp. 155–158 |
| [a5] | E. Garcia-Rio, D.N. Kupeli, M.E. Vázquez-Abal, "On a problem of Osserman in Lorentzian geometry" Diff. Geom. Appl. , 7 (1997) pp. 85–100 |
| [a6] | R. Osserman, "Curvature in the eighties" Amer. Math. Monthly , 97 (1990) pp. 731–756 |
| [a7] | G. Stanilov, V. Videv, "Four dimensional pointwise Osserman manifolds" Abh. Math. Sem. Univ. Hamburg , 68 (1998) pp. 1–6 |
| [a8] | I. Stavrov, "A note on generalized Osserman manifolds" Preprint (1998) |
Osserman conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osserman_conjecture&oldid=15029