Difference between revisions of "Osculating plane"
From Encyclopedia of Mathematics
(Importing text file) |
(Category:Differential geometry) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | ''at a point | + | {{TEX|done}} |
| + | ''at a point $M$ of a curve $l$'' | ||
| − | The plane having contact of order | + | The plane having contact of order $n\geq2$ with $l$ at $M$ (see [[Osculation|Osculation]]). The osculating plane can also be defined as the limit of a variable plane passing through three points of $l$ as these points approach $M$. Usually, a curve intersects the osculating plane at the point of contact (see Fig.). |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/o070560a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/o070560a.gif" /> | ||
| Line 7: | Line 8: | ||
Figure: o070560a | Figure: o070560a | ||
| − | If | + | If $l$ is given by equations |
| − | + | $$x=x(u),\quad y=y(u),\quad z=z(u),$$ | |
then the equation of the osculating plane has the form | then the equation of the osculating plane has the form | ||
| − | + | $$\begin{vmatrix}X-x&Y-y&Z-z\\x'&y'&z'\\x''&y''&z''\end{vmatrix}=0,$$ | |
| − | where | + | where $X,Y,Z$ are moving coordinates and $x,y,z$, $x',y',z'$, $x'',y'',z''$ are calculated at the point of contact. If all three coefficients of $X,Y,Z$ in the equation of the osculating plane vanish, then the osculating plane becomes indefinite (and can coincide with any plane through the tangent line). |
| Line 23: | Line 24: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 31–35</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> D.J. Struik, "Lectures on classical differential geometry" , Dover, reprint (1988) pp. 10ff</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 31–35</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> D.J. Struik, "Lectures on classical differential geometry" , Dover, reprint (1988) pp. 10ff</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | [[Category:Differential geometry]] | ||
Revision as of 19:51, 15 November 2014
at a point $M$ of a curve $l$
The plane having contact of order $n\geq2$ with $l$ at $M$ (see Osculation). The osculating plane can also be defined as the limit of a variable plane passing through three points of $l$ as these points approach $M$. Usually, a curve intersects the osculating plane at the point of contact (see Fig.).
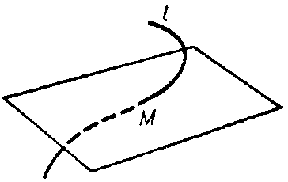
Figure: o070560a
If $l$ is given by equations
$$x=x(u),\quad y=y(u),\quad z=z(u),$$
then the equation of the osculating plane has the form
$$\begin{vmatrix}X-x&Y-y&Z-z\\x'&y'&z'\\x''&y''&z''\end{vmatrix}=0,$$
where $X,Y,Z$ are moving coordinates and $x,y,z$, $x',y',z'$, $x'',y'',z''$ are calculated at the point of contact. If all three coefficients of $X,Y,Z$ in the equation of the osculating plane vanish, then the osculating plane becomes indefinite (and can coincide with any plane through the tangent line).
Comments
References
| [a1] | R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 31–35 |
| [a2] | D.J. Struik, "Lectures on classical differential geometry" , Dover, reprint (1988) pp. 10ff |
How to Cite This Entry:
Osculating plane. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculating_plane&oldid=12865
Osculating plane. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculating_plane&oldid=12865
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article