Osculating paraboloid
of a surface at a point 
The paraboloid that reproduces the shape of the surface near this point up to variables of the second order of smallness with respect to the distance from  . Let
. Let  be a paraboloid (see Fig.) with vertex
be a paraboloid (see Fig.) with vertex  and tangent to the surface at this point, and let
and tangent to the surface at this point, and let  and
and  be the distances of an arbitrary point
be the distances of an arbitrary point  on the paraboloid to the surface and to
on the paraboloid to the surface and to  , respectively.
, respectively.

Figure: o070550a
Then  is said to osculate if
is said to osculate if  as
as 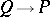 . This does not exclude the degeneration of the paraboloid into a parabolic cylinder or plane. At every point of a regular surface there is a unique osculating paraboloid. Osculating paraboloids can be used to classify the points on a surface (see Elliptic point; Hyperbolic point; Parabolic point; Flat point).
. This does not exclude the degeneration of the paraboloid into a parabolic cylinder or plane. At every point of a regular surface there is a unique osculating paraboloid. Osculating paraboloids can be used to classify the points on a surface (see Elliptic point; Hyperbolic point; Parabolic point; Flat point).
Comments
The osculating paraboloid at  to the surface
to the surface 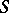 has contact of order three with
has contact of order three with  at
at 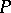 , i.e. the derivatives up to and including order 2 of the difference
, i.e. the derivatives up to and including order 2 of the difference 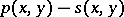 of the functions
of the functions  and
and  describing the paraboloid and the surface are all zero at
describing the paraboloid and the surface are all zero at 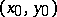 , where
, where 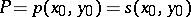 .
.
References
| [a1] | R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 138 |
| [a2] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
Osculating paraboloid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculating_paraboloid&oldid=12753