Oscillation of a function
From Encyclopedia of Mathematics
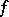on a set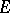 
The difference between the least upper and the greatest lower bounds of the values of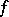 
on 
. In other words, the oscillation of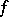 
on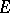 
is given by
 |
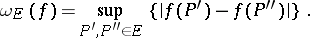If the function is unbounded on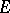 
, its oscillation on 
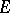is put equal to 
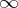. For constant functions on 
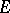(and only for these) the oscillation on 
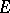is zero. If the function 
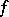is defined on a subset 
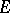of 
, then its oscillation at any point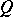 
of the closure of 
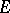is defined by the formula
 |
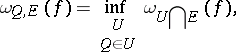where the infimum is taken over all neighbourhoods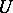 
of 
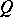. If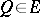 
, then in order that 
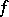be continuous at 
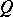with respect to the set 
it is necessary and sufficient that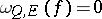 
.
Comments
The function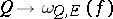 
is called the oscillation function of 
.
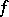References
| [a1] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) pp. 120 |
| [a2] | R.R. Goldberg, "Methods of real analysis" , Blaisdell (1964) pp. 129 |
How to Cite This Entry:
Oscillation of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oscillation_of_a_function&oldid=12236
Oscillation of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oscillation_of_a_function&oldid=12236
This article was adapted from an original article by A.A. Konyushkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article