Orthonormal system

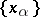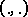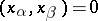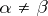An orthonormal system of vectors is a set of vectors in a Euclidean (Hilbert) space with inner product such that if (orthogonality) and 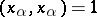(normalization).

M.I. Voitsekhovskii

An orthonormal system of functions is a system 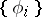of functions in a space 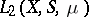which is simultaneously orthogonal and normalized in 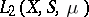, i.e.

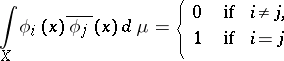(see Normalized system; Orthogonal system). In the mathematical literature, the term "orthogonal system" often means "orthonormal system" ; when studying a given orthogonal system, it is not always crucial whether or not it is normalized. None the less, if the systems are normalized, a clearer formulation is possible for certain theorems on the convergence of a series

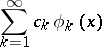in terms of the behaviour of the coefficients . An example of this type of theorem is the Riesz–Fischer theorem: The series

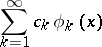with respect to an orthonormal system in 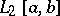converges in the metric of 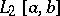if and only if

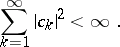References

[1]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Pitman (1981) (Translated from Russian)
[2]	S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951)

A.A. Talalyan

References

[a1]	J. Weidmann, "Linear operators in Hilbert space" , Springer (1980)
[a2]	K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5