Orthogonal transformation
A linear transformation 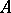 of a Euclidean space preserving the lengths (or, equivalently, the scalar product) of vectors. Orthogonal transformations and only they can transfer an orthonormal basis to an orthonormal one. The equality
of a Euclidean space preserving the lengths (or, equivalently, the scalar product) of vectors. Orthogonal transformations and only they can transfer an orthonormal basis to an orthonormal one. The equality 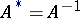 is also a necessary and sufficient condition of orthogonality, where
is also a necessary and sufficient condition of orthogonality, where 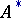 is the conjugate and
is the conjugate and 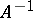 the inverse linear transformation.
the inverse linear transformation.
With respect to an orthonormal basis, orthogonal matrices correspond to orthogonal transformations and only to them. The eigen values of an orthogonal transformation are equal to 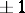 , while the eigen vectors which correspond to different eigen values are orthogonal. The determinant of an orthogonal transformation is equal to
, while the eigen vectors which correspond to different eigen values are orthogonal. The determinant of an orthogonal transformation is equal to 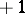 (special orthogonal transformation) or
(special orthogonal transformation) or 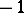 (non-special orthogonal transformation). In the Euclidean plane, every special orthogonal transformation is a rotation, and its matrix in an appropriate orthonormal basis has the form
(non-special orthogonal transformation). In the Euclidean plane, every special orthogonal transformation is a rotation, and its matrix in an appropriate orthonormal basis has the form
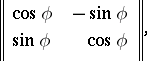 |
where 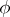 is the angle of the rotation; and every non-special orthogonal transformation is a reflection with respect to a straight line through the origin, and its matrix in an appropriate orthonormal basis has the form
is the angle of the rotation; and every non-special orthogonal transformation is a reflection with respect to a straight line through the origin, and its matrix in an appropriate orthonormal basis has the form
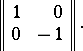 |
In three-dimensional space, every special orthogonal transformation is a rotation around an axis, while every non-special orthogonal transformation is the product of such a rotation and a reflection in a perpendicular plane. In an arbitrary  -dimensional Euclidean space, orthogonal transformations also reduce to rotations and reflections (see Rotation).
-dimensional Euclidean space, orthogonal transformations also reduce to rotations and reflections (see Rotation).
The set of all orthogonal transformations in a Euclidean space is a group with respect to multiplication of transformations — the orthogonal group of the given Euclidean space. The special orthogonal transformations form a normal subgroup in this group (the special orthogonal group).
Comments
See also Orthogonal matrix and Orthogonal group, and the references therein.
Orthogonal transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orthogonal_transformation&oldid=12471