Orlicz space
A Banach space of measurable functions introduced by W. Orlicz [1]. Let  and
and  be a pair of complementary
be a pair of complementary  -functions (see Orlicz class) and let
-functions (see Orlicz class) and let  be a bounded closed set in
be a bounded closed set in  . The Orlicz space
. The Orlicz space  is the set of Lebesgue-measurable functions
is the set of Lebesgue-measurable functions  on
on  for which
for which
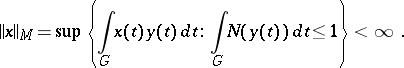 |
An Orlicz space is a complete normed space with respect to the norm 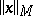 , which is called the Orlicz norm. When
, which is called the Orlicz norm. When 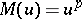 ,
, 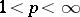 ,
, 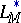 coincides with the Riesz space
coincides with the Riesz space  and, up to a scalar factor,
and, up to a scalar factor, 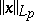 coincides with
coincides with  .
.
If  and
and  are
are  -functions, then the inclusion
-functions, then the inclusion 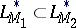 holds if and only if, for a certain
holds if and only if, for a certain  and all sufficiently large
and all sufficiently large  , the inequality
, the inequality  is fulfilled. For every Orlicz space
is fulfilled. For every Orlicz space 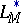 the inclusions
the inclusions  hold. Every summable function belongs to some Orlicz space.
hold. Every summable function belongs to some Orlicz space.
The space  is separable if and only if
is separable if and only if 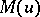 satisfies the
satisfies the  -condition (cf. Orlicz class). In general,
-condition (cf. Orlicz class). In general, 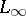 is not dense in
is not dense in 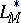 , and the closure of
, and the closure of 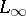 in
in  is denoted by
is denoted by  and is always separable. If
and is always separable. If 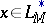 , then
, then
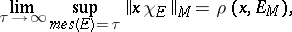 |
where
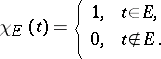 |
If  and
and 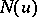 are complementary
are complementary  -functions and
-functions and 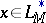 ,
, 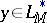 , then the following analogue of the Hölder inequality holds:
, then the following analogue of the Hölder inequality holds:
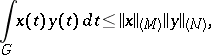 |
where  is the Luxemburg norm. Every continuous linear functional
is the Luxemburg norm. Every continuous linear functional 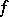 on
on 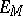 can be represented in the form
can be represented in the form
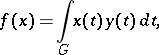 |
where  and
and  .
.
The compactness criteria of M. Riesz and A.N. Kolmogorov for the spaces 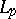 can also be applied to
can also be applied to 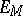 . The following conditions are equivalent:
. The following conditions are equivalent:
1) the space 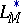 is reflexive;
is reflexive;
2) 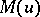 and
and  satisfy the
satisfy the 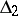 -condition;
-condition;
3) an unconditional basis exists in 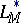 ;
;
4) the Haar system forms an unconditional basis in  ;
;
5) the trigonometric system is a basis in  and the Haar system is a basis in
and the Haar system is a basis in 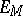 .
.
A sequence space  is defined in the same way, but the properties of
is defined in the same way, but the properties of 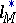 depend on the asymptotics of the function
depend on the asymptotics of the function 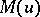 at 0. Many of the geometric properties of
at 0. Many of the geometric properties of 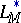 and
and  are studied in [5]; for example, for any function
are studied in [5]; for example, for any function  , the set of all
, the set of all  such that
such that 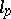 is isomorphically imbeddable in
is isomorphically imbeddable in 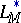 can be found.
can be found.
Orlicz spaces are used in the study of the properties of integral operators, the theory of differentiable functions of several variables and in other areas of analysis.
References
| [1] | W. Orlicz, "Ueber eine gewisse Klasse von Räumen vom Typus 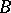 " Bull. Intern. Acad. Pol. Ser. A , 8/9 (1932) pp. 207–220 " Bull. Intern. Acad. Pol. Ser. A , 8/9 (1932) pp. 207–220 |
| [2] | M.A. Krasnosel'skii, Ya.B. Rutitskii, "Convex functions and Orlicz spaces" , Noordhoff (1961) (Translated from Russian) |
| [3] | V.F. Gaposhkin, "Existence of absolute bases in Orlicz spaces" Funct. Anal. Appl. , 1 : 4 (1967) pp. 278–284 Funkts. Anal. i Prilozhen. , 1 : 4 (1967) pp. 26–32 |
| [4] | S.G. Krein, Yu.I. Petunin, E.M. Semenov, "Interpolation of linear operators" , Amer. Math. Soc. (1982) (Translated from Russian) |
| [5] | J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces" , 1–2 , Springer (1977–1979) |
Comments
References
| [a1] | W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971) |
Orlicz space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orlicz_space&oldid=17861