Orlicz-Sobolev space
A natural generalization of the notion of a Sobolev space, where the underlying role of the Lebesgue spaces $L _ { p }$ is played by the more general Orlicz spaces $L _ { \Phi }$ (cf. also Lebesgue space; Orlicz space). Here, $\Phi$ is a Young function (cf. Orlicz–Lorentz space) or an $N$-function, depending on the desired generality of the concept. Various authors use different definitions of the generating function $\Phi$.
The classical setting of the theory of Orlicz spaces can be found, e.g., in [a19], [a11]; the theory of more general modular spaces goes back to H. Nakano [a16] and it has been systematically developed by the Poznań school in the framework of Orlicz–Musielak spaces, see [a15].
Since the 1960s, the need to use spaces of functions with generalized derivatives in Orlicz spaces came from various applications in integral equations, boundary value problems, etc., whenever it is useful to consider wider scales of spaces than those based on $L _ { p }$ (see, e.g. [a3], [a4], [a7], [a8], [a14], [a18] and references therein).
The standard construction of an Orlicz–Sobolev space is as follows. Let $\Omega \subset \mathbf{R} ^ { n }$ be a domain, let $\Phi$ be a classical $N$-function, that is, real-valued function on $[ 0 , + \infty )$, continuous, increasing, convex, and such that $\operatorname { lim } _ { t \rightarrow 0 } \Phi ( t ) / t = 0$, $\operatorname { lim } _ { t \rightarrow + \infty } \Phi ( t ) / t = + \infty$. (Observe that if $| \Omega | < \infty$, then only the behaviour of $\Phi$ at infinity matters.) Let $k \in \mathbf{N}$. Then the Orlicz–Sobolev space $W ^ { k } L _ { \Phi } ( \Omega )$ is the set of measurable functions $f$ on $\Omega$ with generalized (weak) derivatives $D ^ { \alpha } f$ up to the order $k$ (cf. Weak derivative; Generalized function), and equipped with the finite norm
\begin{equation} \tag{a1} \left\| f |_ { W ^{k} L _ { \Phi } ( \Omega ) } \right\| = \sum _ { | \alpha | \leq k } \| D ^ { \alpha } f \| _ { L _ { \Phi } ( \Omega ) }. \end{equation}
Here $\| . \| _ { L _ { \Phi } ( \Omega )}$ is the Luxemburg norm in the Orlicz space $L _ { \Phi } ( \Omega )$. Alternatively, in (a1) one can use the Orlicz norm and any expression equivalent to the summation (such as 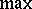 ). Also, it is possible to define anisotropic spaces, considering $\| D ^ { \alpha } f |_{L _ { \Phi _ { \alpha } }} ( \Omega ) \|$, $\alpha \leq k$, where the $\Phi _ { \alpha }$ are $N$-functions. Moreover, one can also consider mixed norms, replacing $\Phi _ { \alpha }$ by $n$-tuples of $N$-functions and various combinations. It is easy to see that $W ^ { k } L _ { \Phi } ( \Omega )$ is a closed subset of a product of the Orlicz spaces $L _ { \Phi } ( \Omega )$, hence it is a Banach space.
). Also, it is possible to define anisotropic spaces, considering $\| D ^ { \alpha } f |_{L _ { \Phi _ { \alpha } }} ( \Omega ) \|$, $\alpha \leq k$, where the $\Phi _ { \alpha }$ are $N$-functions. Moreover, one can also consider mixed norms, replacing $\Phi _ { \alpha }$ by $n$-tuples of $N$-functions and various combinations. It is easy to see that $W ^ { k } L _ { \Phi } ( \Omega )$ is a closed subset of a product of the Orlicz spaces $L _ { \Phi } ( \Omega )$, hence it is a Banach space.
Elementary properties of Orlicz spaces imply that $W ^ { k } L _ { \Phi } ( \Omega )$ is separable if and only if $\Phi$ satisfies the $\Delta _ { 2 }$-condition (cf. Orlicz–Lorentz space). Furthermore, $W ^ { k } L _ { \Phi } ( \Omega )$ is reflexive if and only if both $\Phi$ and the complementary function $\tilde { \Phi }$ to $\Phi$ (that is, $\tilde { \Phi } ( s ) = \operatorname { sup } \{ | s | t - \Phi ( t ) : t \geq 0 \}$) satisfy the $\Delta _ { 2 }$-condition. It is useful to introduce the space $W ^ { k } E _ { \Phi } ( \Omega )$, consisting of the functions with generalized derivatives in $E _ { \Phi } ( \Omega )$, where $E _ { \Phi } ( \Omega )$ is the closure of the set of bounded functions with compact support in $\Omega$. If $\Omega = {\bf R} ^ { n }$, then $C _ { 0 } ^ { \infty }$ is dense in $W ^ { k } E _ { \Phi } ( \Omega )$; further, $C ^ { \infty } ( \Omega ) \cap W ^ { k } E _ { \Phi } ( \Omega )$ is dense in $W ^ { k } E _ { \Phi } ( \Omega )$. Analogues of density theorems known from the theory of Sobolev spaces, with various assumptions about the smoothness of the boundary of the domain in question, can be proved too, thus making it possible to consider alternative definitions. This is important for the standard proof techniques, which work with smooth functions only. (See [a1], [a6], [a10], [a12].)
If $\Omega = {\bf R} ^ { n }$, then one can define the Orlicz–Sobolev potential spaces in a manner quite analogous to the Sobolev case as well as to the case of potential spaces on sufficiently smooth domains. This is also a natural way to define Orlicz–Sobolev spaces of fractional order. The situation here, however, is more delicate than in the $L _ { p }$-based case. Interpolation properties of Orlicz spaces (see, e.g., [a9]) guarantee that $W ^ { k } E _ { \Phi } ( \mathbf{R} ^ { n } )$ (and consequently also spaces on domains with the extension property) can be obtained by interpolation (cf. Interpolation of operators) from a suitable couple of Sobolev spaces provided that both the $N$-function $\Phi$ and its complementary function satisfy the $\Delta _ { 2 }$-condition (or, equivalently, that each Boyd index of $\Phi$ (see [a2]) lies strictly between $1$ and $\infty$). Namely, in this case a Mikhlin-type multiplier theorem holds. Furthermore, the known trace theorems (see [a13], [a17], for instance), identifying the trace space for $W ^ { k } L _ { \Phi } ( \Omega )$, where $\tilde { \Phi }$ satisfies the $\Delta _ { 2 }$-condition, with the subspace of $W ^ { k - 1 } L _ { \Phi } ( \partial \Omega )$ of functions with finite norm
\begin{equation*} \| f \| _ { W ^ { k - 1 } L _ { \Phi } ( \partial \Omega )} + \textbf { inf } \end{equation*}
\begin{equation*} \left\{ \lambda > 0 : \sum _ { | \alpha | = k - 1 } \int _ { \partial \Omega \times \partial \Omega } \Phi \left( \frac { \Delta_{ y - x} F ( x ) } { | y - x | } \right) \eta ( x , y ) \leq 1 \right\}, \end{equation*}
where
\begin{equation*} \Delta _ { h } F ( x ) = F ( x + h ) - F ( x ), \end{equation*}
\begin{equation*} \eta ( x , y ) = | y - x | ^ { 2 - n } d x d y, \end{equation*}
indicate how another "natural" interpolation scale (this time with respect to the smoothness) should look like. The theory, however, is not yet (1998) complete in this area.
In connection with certain applications (imbeddings in finer scales of spaces, entropy and approximation numbers, etc.), attention has been given to logarithmic Orlicz and Orlicz–Sobolev spaces, where the generating function is equivalent to $t ^ { p } \operatorname { log } ^ { \sigma } t$ for large values of $t$ and $1 < p < \infty$. It turns out that these can also be handled using extrapolation of Sobolev spaces, making it thus possible to employ various techniques (e.g. an analytical Fourier approach) known from the theory of Sobolev spaces. A basic reference is [a5].
For a survey of the properties of $W ^ { k } L _ { \Phi } ( \Omega )$, see [a1] and [a12].
References
| [a1] | R.A. Adams, "Sobolev spaces" , Acad. Press (1975) |
| [a2] | D.W. Boyd, "Indices for the Orlicz spaces" Pacific J. Math. , 38 (1971) pp. 315–323 |
| [a3] | T. Donaldson, "Nonlinear elliptic boundary-value problems in Orlicz–Sobolev spaces" J. Diff. Eq. , 10 (1971) pp. 507–528 |
| [a4] | T. Donaldson, "Inhomogeneous Orlicz–Sobolev spaces and nonlinear parabolic initial value problems" J. Diff. Eq. , 16 (1974) pp. 201–256 |
| [a5] | D.E. Edmunds, H. Triebel, "Logarithmic Sobolev spaces and their applications to spectral theory" Proc. London Math. Soc. , 71 : 3 (1995) pp. 333–371 |
| [a6] | A. Fougères, "Approximation dans les espaces de Sobolev et de Sobolev–Orlicz" C.R. Acad. Sci. Paris Ser. A , 274 (1972) pp. 479–482 |
| [a7] | J.-P. Gossez, "Nonlinear elliptic boundary value problems for equations with rapidly (or slowly) increasing coefficients" Trans. Amer. Math. Soc. , 190 (1974) pp. 163–205 |
| [a8] | J.-P. Gossez, V. Mustonen, "Variational inequalities in Orlicz–Sobolev spaces" Nonlinear Anal. Theory Meth. Appl. , 11 (1987) pp. 379–392 |
| [a9] | J. Gustavsson, J. Peetre, "Interpolation of Orlicz spaces" Studia Math. , 60 (1977) pp. 33–59 |
| [a10] | H. Hudzik, "The problems of separability, duality, reflexivity and of comparison for generalized Orlicz–Sobolev spaces $W_ { m } ^ { k } ( \Omega )$" Comment. Math. Helvetici , 21 (1979) pp. 315–324 |
| [a11] | M.A. Krasnosel'skii, Ya.B. Rutitskii, "Convex functions and Orlicz spaces" , Noordhoff (1961) (In Russian) |
| [a12] | A. Kufner, O. John, S. Fučik, "Function spaces" , Acad. Prague (1977) |
| [a13] | M.-Th. Lacroix, "Espaces d'interpolation et de traces des espaces de Sobolev–Orlicz d'ordre 1" C.R. Acad. Sci. Paris Ser. A , 280 (1975) pp. 271–274 |
| [a14] | R. Landes, V. Mustonen, "Pseudo-monotone mappings in Sobolev–Orlicz spaces and nonlinear boundary value problems on unbounded domains" J. Math. Anal. Appl. , 88 (1982) pp. 25–36 |
| [a15] | J. Musielak, "Orlicz spaces and modular spaces" , Lecture Notes Math. , 1034 , Springer (1983) |
| [a16] | H. Nakano, "Modulared semi-ordered linear spaces" , Maruzen (1950) |
| [a17] | G. Palmieri, "Alcune disuguaglianze per derivate intermedie negli spazi di Orlicz–Sobolev e applicazioni" Rend. Accad. Sci. Fis. Mat. IV. Ser., Napoli , 46 (1979) pp. 633–652 (In Italian) |
| [a18] | P.A. Vuillermot, "Hölder-regularity for the solutions of strongly nonlinear eigenvalue problems on Orlicz–Sobolev spaces" Houston J. Math. , 13 (1987) pp. 281–287 |
| [a19] | A.C. Zaanen, "Linear analysis" , Noordhoff (1953) |
Orlicz-Sobolev space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orlicz-Sobolev_space&oldid=50710