Ordinary differential equations, property C for
Let
 |
 |
and let  be a real-valued function,
be a real-valued function,
 |
Consider the problem
 |
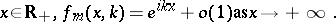 |
This problem has a unique solution, which is called the Jost function.
Define also the solutions to the problem
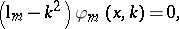 |
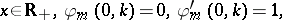 |
and to the problem
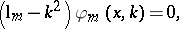 |
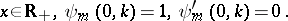 |
Assume 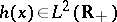 and
and
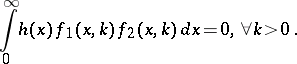 | (a1) |
If (a1) implies  , then one says that the pair
, then one says that the pair 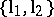 has property
has property 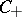 .
.
Let 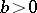 be an arbitrary fixed number, let
be an arbitrary fixed number, let 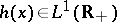 and assume
and assume
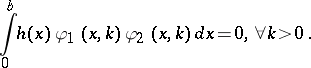 | (a2) |
If (a2) implies 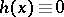 , then one says that the pair
, then one says that the pair 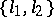 has property
has property 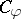 .
.
Similarly one defines property 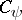 .
.
It is proved in [a1] that the pair 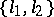 has property
has property 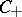 if
if 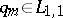 ,
, 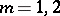 .
.
It is proved in [a2] that the pair 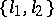 has properties
has properties 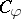 and
and 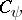 .
.
However, if 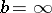 , then, in general, property
, then, in general, property 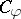 fails to hold for a pair
fails to hold for a pair 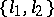 . This means that there exist a function
. This means that there exist a function 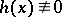 ,
, 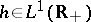 , and two potentials
, and two potentials 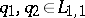 , such that (a1) holds for all
, such that (a1) holds for all 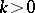 .
.
In [a2] many applications of properties 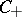 ,
, 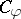 and
and 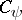 to inverse problems are presented.
to inverse problems are presented.
For instance, suppose that the 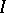 -function, defined as
-function, defined as 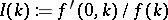 , is known for all
, is known for all 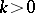 ,
, 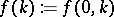 and
and 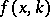 is the Jost function corresponding to a potential
is the Jost function corresponding to a potential 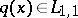 .
.
The function 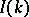 is known as the impedance function [a4], and it can be measured in some problems of electromagnetic probing of the Earth. The inverse problem (IP) is: Given
is known as the impedance function [a4], and it can be measured in some problems of electromagnetic probing of the Earth. The inverse problem (IP) is: Given  for all
for all 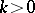 , can one recover
, can one recover 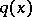 uniquely?
uniquely?
This problem was solved in [a4], but in [a1] and [a2] a new approach to this and many other inverse problems is developed. This new approach is sketched below.
Suppose that there are two potentials, 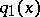 and
and 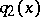 , which generate the same data
, which generate the same data 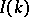 . Subtract from the equation
. Subtract from the equation 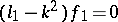 the equation
the equation 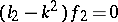 , and denote
, and denote 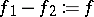 ,
, 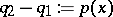 , to get
, to get 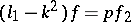 . Multiply this equation by
. Multiply this equation by 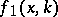 , integrate over
, integrate over 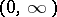 and then by parts. The assumption
and then by parts. The assumption
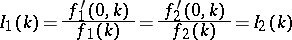 |
implies 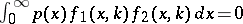 ,
, 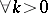 .
.
Using property 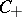 one concludes
one concludes 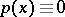 , that is,
, that is, 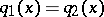 . This is a typical scheme for proving uniqueness theorems using property
. This is a typical scheme for proving uniqueness theorems using property 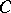 .
.
References
| [a1] | A.G. Ramm, "Property C for ODE and applications to inverse scattering" Z. Angew. Anal. , 18 : 2 (1999) pp. 331–348 |
| [a2] | A.G. Ramm, "Property C for ODE and applications to inverse problems" A.G. Ramm (ed.) P.N. Shivakumar (ed.) A.V. Strauss (ed.) , Operator Theory And Its Applications , Fields Inst. Commun. , 25 , Amer. Math. Soc. (2000) pp. 15–75 |
| [a3] | A.G. Ramm, "Inverse scattering problem with part of the fixed-energy phase shifts" Comm. Math. Phys. , 207 : 1 (1999) pp. 231–247 |
| [a4] | A.G. Ramm, "Recovery of the potential from 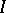 -function" Math. Rept. Acad. Sci. Canada , 9 (1987) pp. 177–182 -function" Math. Rept. Acad. Sci. Canada , 9 (1987) pp. 177–182 |
Ordinary differential equations, property C for. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ordinary_differential_equations,_property_C_for&oldid=18905