Ordinal number
transfinite number, ordinal
The order type of a well-ordered set. This notion was introduced by G. Cantor in 1883 (see [2]). For instance, the ordinal number of the set of all positive integers ordered by the relation 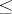 is
is 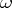 . The ordinal number of the set consisting of
. The ordinal number of the set consisting of 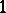 and of the numbers of the form
and of the numbers of the form 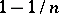 , for
, for 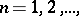 ordered by the relation
ordered by the relation 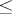 is
is  . One says that an ordinal number
. One says that an ordinal number  is equal to (less than) an ordinal number
is equal to (less than) an ordinal number 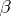 ,
, 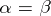 (
(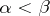 ) if a set of type
) if a set of type 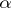 is similar to (a proper segment of) a set of type
is similar to (a proper segment of) a set of type 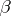 . For arbitrary ordinal numbers
. For arbitrary ordinal numbers 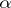 and
and  one and only one of the following possibilities holds: either
one and only one of the following possibilities holds: either 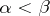 , or
, or 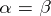 , or
, or 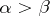 . The set
. The set 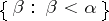 of all ordinal numbers less than
of all ordinal numbers less than 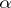 is well-ordered with type
is well-ordered with type 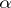 by the relation
by the relation 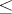 . Moreover, any set of ordinal numbers is well-ordered by the relation
. Moreover, any set of ordinal numbers is well-ordered by the relation 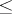 , i.e. any non-empty set of ordinal numbers contains a least ordinal number. For any set
, i.e. any non-empty set of ordinal numbers contains a least ordinal number. For any set 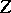 of ordinal numbers there exists an ordinal number greater than any ordinal number from
of ordinal numbers there exists an ordinal number greater than any ordinal number from 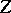 . Accordingly, the set of all ordinal numbers does not exist. The smallest of the ordinal numbers following an ordinal number
. Accordingly, the set of all ordinal numbers does not exist. The smallest of the ordinal numbers following an ordinal number 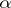 is called the successor of
is called the successor of 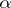 and is denoted by
and is denoted by 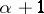 . The ordinal number
. The ordinal number 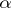 is called the predecessor of the ordinal number
is called the predecessor of the ordinal number 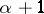 . An ordinal number is called a limit (ordinal) number if it does not have a predecessor. Thus,
. An ordinal number is called a limit (ordinal) number if it does not have a predecessor. Thus,  is a limit number. Any ordinal number can be represented in the form
is a limit number. Any ordinal number can be represented in the form 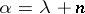 , where
, where 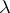 is a limit number and
is a limit number and  is an integer, the sum is understood in the sense of addition of order types (cf. Order type).
is an integer, the sum is understood in the sense of addition of order types (cf. Order type).
A transfinite sequence of type 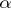 , or an
, or an 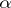 -sequence, is a function
-sequence, is a function 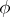 defined on
defined on 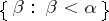 . If the values of this sequence are ordinal numbers and
. If the values of this sequence are ordinal numbers and 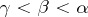 implies that
implies that 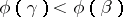 , then it is called an ascending sequence. Let
, then it is called an ascending sequence. Let 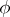 denote a
denote a 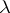 -sequence, where
-sequence, where 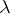 is a limit number. The least of the ordinal numbers greater than any
is a limit number. The least of the ordinal numbers greater than any 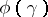 , where
, where 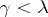 , is called the limit of the sequence
, is called the limit of the sequence 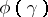 for
for 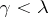 and is denoted by
and is denoted by 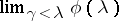 . For instance,
. For instance, 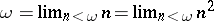 . An ordinal number
. An ordinal number 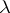 is cofinal to a limit number
is cofinal to a limit number 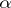 if
if 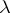 is the limit of an ascending
is the limit of an ascending 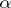 -sequence:
-sequence: 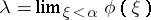 . The ordinal number
. The ordinal number 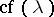 is the least ordinal number to which
is the least ordinal number to which 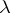 is cofinal.
is cofinal.
An ordinal number is called regular if it is not cofinal to any smaller ordinal number, otherwise it is called singular. An infinite ordinal number is called an initial ordinal number of cardinality  if it is the least among the ordinal numbers of cardinality
if it is the least among the ordinal numbers of cardinality  (i.e. among the order types of well-ordered sets of cardinality
(i.e. among the order types of well-ordered sets of cardinality  ). Hence
). Hence 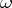 is the least initial number. The initial ordinal number of power
is the least initial number. The initial ordinal number of power  is denoted by
is denoted by 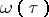 . The set
. The set 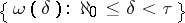 of all initial ordinal numbers of infinite cardinality less than
of all initial ordinal numbers of infinite cardinality less than  is well-ordered. If the ordinal number
is well-ordered. If the ordinal number 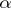 is its order type, then one puts
is its order type, then one puts 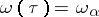 . Thus, every initial ordinal number is provided with an index equal to the order type of the set of all initial ordinal numbers less than it. In particular,
. Thus, every initial ordinal number is provided with an index equal to the order type of the set of all initial ordinal numbers less than it. In particular, 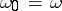 . Different indices correspond to different initial numbers. Each ordinal number
. Different indices correspond to different initial numbers. Each ordinal number 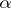 is the index of some initial number. If
is the index of some initial number. If 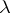 is a limit ordinal number, then
is a limit ordinal number, then 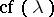 is a regular initial number.
is a regular initial number.
An initial number 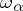 is called weakly inaccessible if it is regular and its index
is called weakly inaccessible if it is regular and its index 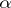 is a limit number. For instance,
is a limit number. For instance, 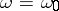 is weakly inaccessible, but
is weakly inaccessible, but 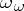 is singular and, thus, is not weakly inaccessible. If
is singular and, thus, is not weakly inaccessible. If 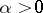 , then
, then 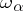 is weakly inaccessible if and only if
is weakly inaccessible if and only if 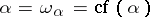 .
.
Weakly-inaccessible ordinal numbers allow a classification similar to the classification of inaccessible cardinal numbers (cf. Cardinal number). The sum and the product of two ordinal numbers is an ordinal number. If the set of indices is well-ordered, then the well-ordered sum of ordinal numbers is an ordinal number. One can also introduce the operation of raising to a power, by transfinite induction: 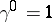 ,
, 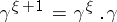 ,
, 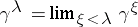 , where
, where 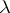 is a limit number. The number
is a limit number. The number 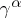 is called a power of a number
is called a power of a number 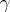 ,
, 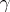 is the base of the power and
is the base of the power and 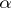 is the exponent of the power. For example, if
is the exponent of the power. For example, if 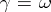 ,
, 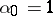 , one obtains
, one obtains 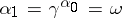 ,
,  ,
, 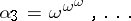 . The limit of this sequence,
. The limit of this sequence, 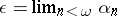 , is the least critical number of the function
, is the least critical number of the function 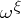 , i.e. the least ordinal number
, i.e. the least ordinal number 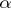 among those for which
among those for which 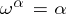 . Numbers
. Numbers 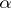 for which this equality holds are called epsilon-ordinals.
for which this equality holds are called epsilon-ordinals.
Raising to a power can be used to represent ordinal numbers in a form resembling decimal representation of positive integers. If 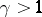 ,
, 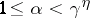 , then there exists a positive integer
, then there exists a positive integer  and sequences
and sequences 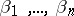 and
and 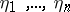 such that
such that
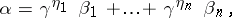 | (1) |
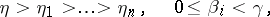 | (2) |
for 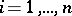 . Formula (1) for the numbers
. Formula (1) for the numbers 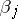 and
and 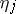 satisfying the conditions (2) is called the representation of the ordinal number
satisfying the conditions (2) is called the representation of the ordinal number 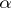 in the base
in the base 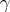 . The numbers
. The numbers  are called the digits, and the numbers
are called the digits, and the numbers 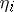 are called the exponents of this representation. The representation of an ordinal number in a given base is unique. The representation of ordinal numbers in the base
are called the exponents of this representation. The representation of an ordinal number in a given base is unique. The representation of ordinal numbers in the base 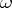 is used to define the natural sum and the natural product of ordinal numbers.
is used to define the natural sum and the natural product of ordinal numbers.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [2] | G. Cantor, "Contributions to the founding of the theory of transfinite numbers" , Dover, reprint (1952) (Translated from German) |
| [3] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [4] | K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968) |
| [5] | W. Sierpiński, "Cardinal and ordinal numbers" , PWN (1958) |
Comments
The ordinal 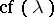 , the least ordinal number to which
, the least ordinal number to which 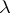 is cofinal, is called the cofinality of
is cofinal, is called the cofinality of 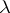 .
.
The ordinal number 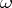 and (by the axiom of choice) each initial ordinal number with a successor-index are regular. Initial ordinal numbers with a limit-index are singular, in general. More precisely, if the axioms of
and (by the axiom of choice) each initial ordinal number with a successor-index are regular. Initial ordinal numbers with a limit-index are singular, in general. More precisely, if the axioms of  set theory are consistent, they remain so after the addition of the axiom stating that all initials with limit-index
set theory are consistent, they remain so after the addition of the axiom stating that all initials with limit-index 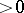 are singular. Thus, the axioms of
are singular. Thus, the axioms of 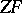 , if consistent, cannot prove that there are any weakly-inaccessible ordinal numbers other than
, if consistent, cannot prove that there are any weakly-inaccessible ordinal numbers other than  .
.
For countable ordinal numbers see also Descriptive set theory.
References
| [a1] | K. Kuratowski, "Introduction to set theory and topology" , Pergamon (1972) (Translated from Polish) |
| [a2] | T.J. Jech, "Set theory" , Acad. Press (1978) (Translated from German) |
| [a3] | J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) ((especially the article of D.A. Martin on Descriptive set theory)) |
| [a4] | A. Levy, "Basic set theory" , Springer (1979) |
Ordinal number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ordinal_number&oldid=15565