Ordered group
A group 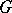 with an order relation
with an order relation 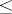 such that for any
such that for any 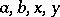 in
in 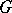 the inequality
the inequality 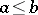 entails
entails  . If the order is total (respectively, partial), one speaks of a totally ordered group (respectively, a partially ordered group).
. If the order is total (respectively, partial), one speaks of a totally ordered group (respectively, a partially ordered group).
An order homomorphism of a (partially) ordered group 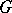 into an ordered group
into an ordered group 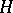 is a homomorphism
is a homomorphism  of
of  into
into 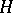 such that
such that 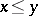 ,
, 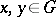 , implies
, implies 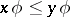 in
in 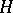 . The kernels of order homomorphisms are the convex normal subgroups (cf. Convex subgroup; Normal subgroup). The set of right cosets of a totally ordered group
. The kernels of order homomorphisms are the convex normal subgroups (cf. Convex subgroup; Normal subgroup). The set of right cosets of a totally ordered group 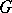 with respect to a convex subgroup
with respect to a convex subgroup  is totally ordered by putting
is totally ordered by putting 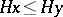 if and only if
if and only if 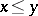 . If
. If 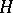 is a convex normal subgroup of a totally ordered group, then this order relation turns the quotient group
is a convex normal subgroup of a totally ordered group, then this order relation turns the quotient group 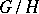 into a totally ordered group.
into a totally ordered group.
The system 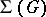 of convex subgroups of a totally ordered group possesses the following properties: a)
of convex subgroups of a totally ordered group possesses the following properties: a) 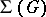 is totally ordered by inclusion and closed under intersections and unions; b)
is totally ordered by inclusion and closed under intersections and unions; b) 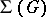 is infra-invariant, i.e. for any
is infra-invariant, i.e. for any 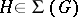 and any
and any 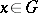 one has
one has 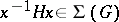 ; c) if
; c) if 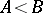 is a jump in
is a jump in 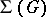 , i.e.
, i.e. 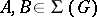 ,
, 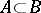 , and there is no convex subgroup between them, then
, and there is no convex subgroup between them, then 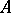 is normal in
is normal in 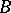 , the quotient group
, the quotient group 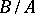 is an Archimedean group and
is an Archimedean group and
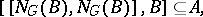 |
where 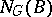 is the normalizer of
is the normalizer of 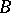 in
in 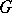 (cf. Normalizer of a subset); and d) all subgroups of
(cf. Normalizer of a subset); and d) all subgroups of 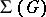 are strongly isolated, i.e. for any finite set
are strongly isolated, i.e. for any finite set 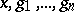 in
in 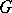 and any subgroup
and any subgroup 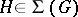 the relation
the relation
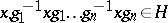 |
entails 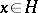 .
.
An extension 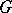 of an ordered group
of an ordered group 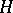 by an ordered group (cf. Extension of a group) is an ordered group if the order in
by an ordered group (cf. Extension of a group) is an ordered group if the order in 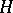 is stable under all inner automorphisms of
is stable under all inner automorphisms of  . An extension
. An extension 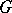 of an ordered group
of an ordered group 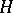 by a finite group is an ordered group if
by a finite group is an ordered group if 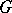 is torsion-free and if the order in
is torsion-free and if the order in 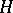 is stable under all inner automorphisms of
is stable under all inner automorphisms of 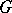 .
.
The order type of a countable ordered group has the form 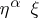 , where
, where 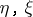 are the order types of the set of integers and of rational numbers, respectively, and
are the order types of the set of integers and of rational numbers, respectively, and 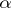 is an arbitrary countable ordinal. Every ordered group
is an arbitrary countable ordinal. Every ordered group 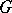 is a topological group relative to the interval topology, in which a base of open sets consists of the open intervals
is a topological group relative to the interval topology, in which a base of open sets consists of the open intervals
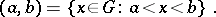 |
A convex subgroup of an ordered group is open in this topology.
References
| [1] | A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Israel Program Sci. Transl. (1974) (Translated from Russian) |
Comments
If the order relation on the partially ordered group defines a lattice (i.e. for all 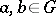 there exists a greatest lower bound
there exists a greatest lower bound 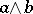 and a least upper bound
and a least upper bound 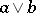 ), then one speaks of a lattice-ordered group or
), then one speaks of a lattice-ordered group or 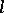 -group; cf. also Ordered semi-group. These turn up naturally in many branches of mathematics. For a survey of the current state-of-the-art in this field see [a1]–[a3].
-group; cf. also Ordered semi-group. These turn up naturally in many branches of mathematics. For a survey of the current state-of-the-art in this field see [a1]–[a3].
References
| [a1] | M. Anderson, T. Feil, "Lattice-ordered groups. An introduction" , Reidel (1988) |
| [a2] | A.M.W. Glass (ed.) W.Ch. Holland (ed.) , Lattice-ordered groups. Advances and techniques , Kluwer (1989) |
| [a3] | J. Martinez (ed.) , Ordered algebraic structures , Kluwer (1989) |
Ordered group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ordered_group&oldid=16970