Orderable group

A group on which a total order (cf. Totally ordered group) can be introduced such that entails for any . A group is orderable as a group if and only if there exists a subset with the properties: 1) ; 2) , 3) ; 4) 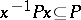for any .

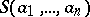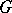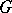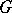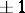Let be the normal sub-semi-group of generated by . The group is orderable as a group if and only if for any finite set of elements in , different from the unit element, numbers can be found, equal to , such that the sub-semi-group 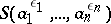does not contain the unit element. Every orderable group is a group with unique root extraction. Abelian torsion-free groups, locally nilpotent torsion-free groups, free, and free solvable groups are orderable groups. Two-step solvable groups such that for every non-unit element , , 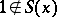are orderable groups.

The class of orderable groups is closed under taking subgroups and direct products; it is locally closed, and consequently, a quasi-variety. A free product of orderable groups is again an orderable group.

References

[1]	A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Israel Program Sci. Transl. (1974) (Translated from Russian)
[2]	L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963)