Order topology
The topology 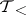 on a linearly ordered set
on a linearly ordered set 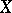 , with linear order
, with linear order  , which has a base consisting of all possible intervals of
, which has a base consisting of all possible intervals of 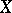 .
.
Comments
Here "interval" is used in the sense of "open interval" , i.e. a set of the form
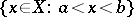 |
where 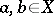 (or possibly
(or possibly 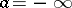 and/or
and/or 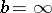 ). The order topology may be considered on partially ordered as well as linearly ordered sets; on a linearly ordered set it coincides with the interval topology which has the closed intervals
). The order topology may be considered on partially ordered as well as linearly ordered sets; on a linearly ordered set it coincides with the interval topology which has the closed intervals
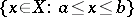 |
as a subbase for the closed sets, but in general it is different. On a complete linearly ordered set, the order topology is characterized by order convergence: that is, a net (see Generalized sequence) 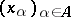 converges to a point
converges to a point  if and only if there are an increasing net
if and only if there are an increasing net 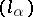 and a decreasing net
and a decreasing net 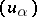 , indexed by the same directed set
, indexed by the same directed set 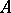 , such that
, such that 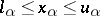 for all
for all 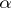 and
and 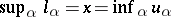 .
.
References
| [a1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [a2] | O. Frink, "Topology in lattices" Trans. Amer. Math. Soc. , 51 (1942) pp. 569–582 |
| [a3] | A.J. Ward, "On relations between certain intrinsic topologies in partially ordered sets" Proc. Cambridge Philos. Soc. , 51 (1955) pp. 254–261 |
Order topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Order_topology&oldid=15011