Order relation
comparison of functions, 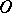 -
- relations, asymptotic relations
relations, asymptotic relations
A notion arising in studies on the behaviour of a function with respect to another function in a neighbourhood of some point (this point may be infinite).
Let 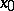 be a limit point of a set
be a limit point of a set 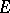 . If for two functions
. If for two functions 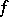 and
and 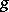 there exist constants
there exist constants 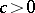 and
and 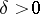 such that
such that 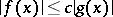 for
for 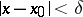 ,
, 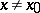 , then
, then 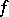 is called a function which is bounded in comparison with
is called a function which is bounded in comparison with 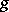 in some deleted neighbourhood of
in some deleted neighbourhood of 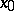 , and this is written as
, and this is written as
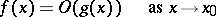 |
(read "f is of the order of g" ); 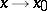 means that the considered property holds only in some deleted neighbourhood of
means that the considered property holds only in some deleted neighbourhood of 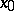 . This definition can be naturally used when
. This definition can be naturally used when 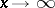 ,
, 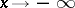 .
.
If two functions 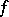 and
and 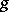 are such that
are such that 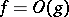 and
and 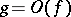 as
as 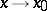 , then they are called functions of the same order as
, then they are called functions of the same order as 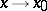 . For instance, if two functions
. For instance, if two functions 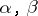 are such that
are such that 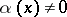 ,
, 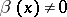 if
if 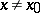 and if the limit
and if the limit
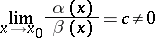 |
exists, then they are of the same order as 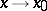 .
.
Two functions 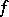 and
and 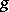 are called equivalent (asymptotically equal) as
are called equivalent (asymptotically equal) as 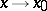 (written as
(written as 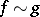 ) if in some neighbourhood of
) if in some neighbourhood of 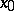 , except maybe the point
, except maybe the point 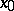 itself, a function
itself, a function 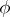 is defined such that
is defined such that
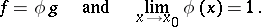 | (*) |
The condition of equivalency of two functions is symmetric, i.e. if 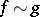 , then
, then 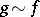 as
as 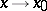 , and transitive, i.e. if
, and transitive, i.e. if  and
and 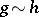 , then
, then 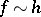 as
as 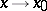 . If in some neighbourhood of the point
. If in some neighbourhood of the point 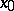 the inequalities
the inequalities 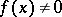 ,
, 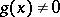 hold for
hold for 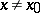 , then (*) is equivalent to any of the following conditions:
, then (*) is equivalent to any of the following conditions:
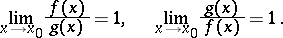 |
If 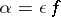 where
where 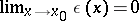 , then
, then 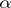 is said to be an infinitely-small function with respect to
is said to be an infinitely-small function with respect to 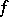 , and one writes
, and one writes
 |
(read "a is of lower order than f" ). If 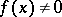 when
when 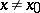 , then
, then 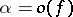 if
if 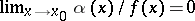 . If
. If 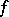 is an infinitely-small function for
is an infinitely-small function for  , one says that the function
, one says that the function 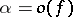 is an infinitely-small function of higher order than
is an infinitely-small function of higher order than 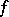 as
as 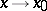 . If
. If 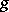 and
and 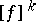 are quantities of the same order, then one says that
are quantities of the same order, then one says that 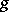 is a quantity of order
is a quantity of order 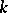 with respect to
with respect to 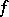 . All formulas of the above type are called asymptotic estimates; they are especially interesting for infinitely-small and infinitely-large functions.
. All formulas of the above type are called asymptotic estimates; they are especially interesting for infinitely-small and infinitely-large functions.
Examples: 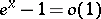 (
(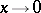 );
); 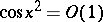 ;
; 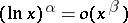 (
(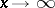 ;
; 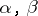 any positive numbers);
any positive numbers); 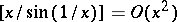 (
(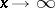 ).
).
Here are some properties of the symbols  and
and 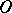 :
:
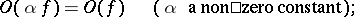 |
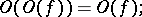 |
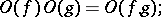 |
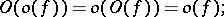 |
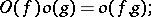 |
if 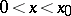 and
and 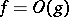 , then
, then
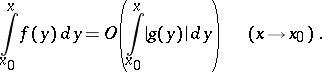 |
Formulas containing the symbols  and
and 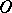 are read only from the left to the right; however, this does not exclude that certain formulas remain true when read from the right to the left. The symbols
are read only from the left to the right; however, this does not exclude that certain formulas remain true when read from the right to the left. The symbols  and
and  for functions of a complex variable and for functions of several variables are introduced in the same way as it was done above for functions of one real variable.
for functions of a complex variable and for functions of several variables are introduced in the same way as it was done above for functions of one real variable.
Comments
The symbols  and
and  ( "little oh symbollittle oh" and "big Oh symbolbig Oh" ) were introduced by E. Landau.
( "little oh symbollittle oh" and "big Oh symbolbig Oh" ) were introduced by E. Landau.
References
| [a1] | G.H. Hardy, "A course of pure mathematics" , Cambridge Univ. Press (1975) |
| [a2] | E. Landau, "Grundlagen der Analysis" , Akad. Verlagsgesellschaft (1930) |
Order relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Order_relation&oldid=16014