Order (on a set)
order relation
A binary relation on some set 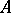 , usually denoted by the symbol
, usually denoted by the symbol 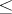 and having the following properties: 1)
and having the following properties: 1) 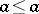 (reflexivity); 2) if
(reflexivity); 2) if 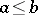 and
and 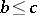 , then
, then 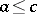 (transitivity); 3) if
(transitivity); 3) if 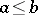 and
and 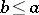 , then
, then 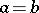 (anti-symmetry). If
(anti-symmetry). If  is an order, then the relation
is an order, then the relation 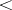 defined by
defined by 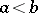 when
when 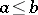 and
and 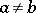 is called a strict order. A strict order can be defined as a relation having the properties 2) and 3'):
is called a strict order. A strict order can be defined as a relation having the properties 2) and 3'): 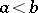 and
and 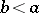 cannot occur simultaneously. The expression
cannot occur simultaneously. The expression 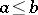 is usually read as "a is less than or equal to b" or "b is greater than or equal to a" , and
is usually read as "a is less than or equal to b" or "b is greater than or equal to a" , and 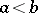 is read as "a is less than b" or "b is greater than a" . The order is called total if for any
is read as "a is less than b" or "b is greater than a" . The order is called total if for any 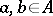 either
either 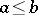 or
or 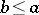 . A relation which has the properties 1) and 2) is called a pre-order or a quasi-order. If
. A relation which has the properties 1) and 2) is called a pre-order or a quasi-order. If 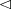 is a quasi-order, then the relation
is a quasi-order, then the relation 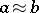 defined by the conditions
defined by the conditions 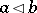 and
and 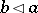 is an equivalence. On the quotient set by this equivalence one can define an order by setting
is an equivalence. On the quotient set by this equivalence one can define an order by setting 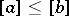 , where
, where 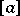 is the class containing the element
is the class containing the element  , if
, if 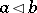 . For examples and references see Partially ordered set.
. For examples and references see Partially ordered set.
Comments
A total order is also called a linear order, and a set equipped with a total order is sometimes called a chain or totally ordered set. For emphasis, an order which is not (necessarily) total is often called a partial order; some writers use the notation 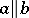 to indicate that neither
to indicate that neither 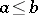 nor
nor 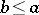 holds.
holds.
Order (on a set). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Order_(on_a_set)&oldid=16903