Order
The order of an algebraic curve 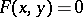 , where
, where 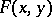 is a polynomial in
is a polynomial in  and
and 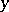 , is the highest degree of the terms of this polynomial. For instance, the ellipse
, is the highest degree of the terms of this polynomial. For instance, the ellipse 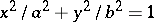 is a curve of order two, and the lemniscate
is a curve of order two, and the lemniscate 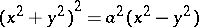 is a curve of order four (cf. Algebraic curve).
is a curve of order four (cf. Algebraic curve).
The order of an infinitesimal quantity 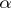 with respect to an infinitesimal quantity
with respect to an infinitesimal quantity 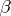 is (if it exists) the number
is (if it exists) the number  such that the limit
such that the limit 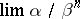 exists and is not infinite or equal to zero. For instance,
exists and is not infinite or equal to zero. For instance, 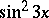 as
as 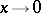 is an infinitesimal of order two with respect to
is an infinitesimal of order two with respect to  since
since 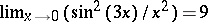 . One says that
. One says that  is an infinitesimal of higher order than
is an infinitesimal of higher order than 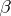 if
if 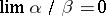 , and of lower order than
, and of lower order than 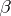 if
if 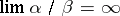 . Analogously one can define the orders of infinitely large quantities (cf. Infinitesimal calculus).
. Analogously one can define the orders of infinitely large quantities (cf. Infinitesimal calculus).
The order of a zero (respectively, a pole)  of a function
of a function 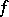 is the number
is the number  such that the limit
such that the limit 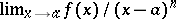 (respectively,
(respectively, 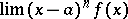 ) exists and is not infinite or equal to zero (cf. e.g. Analytic function; Meromorphic function; Pole (of a function); Rational function).
) exists and is not infinite or equal to zero (cf. e.g. Analytic function; Meromorphic function; Pole (of a function); Rational function).
The order of a derivative is the number of times one has to differentiate a function to obtain this derivative. For instance, 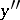 is a derivative of order two,
is a derivative of order two, 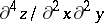 is a derivative of order four. Similarly the order of a differential is defined (cf. Differential calculus).
is a derivative of order four. Similarly the order of a differential is defined (cf. Differential calculus).
The order of a differential equation is the highest order of the derivatives in it. For example, 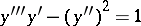 is an equation of order three,
is an equation of order three, 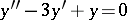 is an equation of order two (cf. Differential equation, ordinary).
is an equation of order two (cf. Differential equation, ordinary).
The order of a square matrix is the number of its rows or columns (cf. Matrix).
The order of a finite group is the number of elements in the group (cf. Finite group). If the group 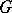 is infinite, one says that it is a group of infinite order. One should not confuse the order of a group with an order on a group (see Ordered group; Partially ordered group).
is infinite, one says that it is a group of infinite order. One should not confuse the order of a group with an order on a group (see Ordered group; Partially ordered group).
The order of an element of a group is the positive integer equal to the number of elements of the cyclic subgroup generated by this element, or to 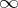 if this subgroup is infinite (cf. also Cyclic group). In the last case the element is of infinite order. If the order of an element
if this subgroup is infinite (cf. also Cyclic group). In the last case the element is of infinite order. If the order of an element  is finite and equal to
is finite and equal to  , then
, then  is the least among the numbers for which
is the least among the numbers for which 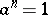 .
.
A right order in a ring 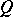 is a subring
is a subring 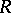 of
of  such that for any
such that for any 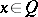 there are
there are 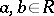 such that
such that 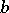 is invertible in
is invertible in 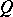 and
and 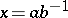 . In other words,
. In other words, 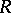 is a subring of
is a subring of 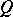 such that
such that 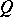 is a classical right ring of fractions of
is a classical right ring of fractions of 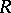 (see Fractions, ring of).
(see Fractions, ring of).
If in some studies or calculations all powers starting with the 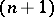 -st of some small quantity are neglected, one says that this study or calculation is carried out up to quantities of order
-st of some small quantity are neglected, one says that this study or calculation is carried out up to quantities of order  . For example, in studies of small oscillations of a string the terms with second and higher degrees of deflection and its derivatives are neglected, as a result one obtains a linear equation (linearization of the problem).
. For example, in studies of small oscillations of a string the terms with second and higher degrees of deflection and its derivatives are neglected, as a result one obtains a linear equation (linearization of the problem).
The word "order" is also used in the calculus of differences (differences of different order, cf. Finite-difference calculus), in the theory of many special functions (e.g. cylinder functions of order  ), etc.
), etc.
In measurements one speaks about a quantity of order 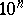 , which means that it is included between
, which means that it is included between 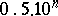 and
and 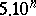 .
.
Comments
The above does not exhaust the many meanings in which the word "order" is used in mathematics.
If 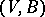 is a balanced incomplete block design, or design with parameters
is a balanced incomplete block design, or design with parameters  ,
, 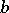 ,
,  ,
, 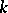 ,
, 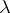 (see Block design), then
(see Block design), then 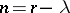 is called the order of the design.
is called the order of the design.
A finite projective plane is of order 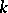 if each line has precisely
if each line has precisely 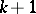 points (and there are (hence) precisely
points (and there are (hence) precisely 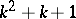 points and
points and 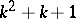 lines).
lines).
Let 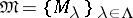 ,
, 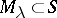 , be a covering of a subset
, be a covering of a subset 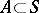 , i.e.
, i.e. 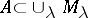 . The covering is said to be of order
. The covering is said to be of order 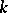 if
if 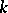 is the least integer such that any subfamily of
is the least integer such that any subfamily of 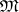 consisting of
consisting of 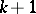 elements has empty intersection.
elements has empty intersection.
Let 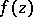 be a transcendental entire function (cf. Entire function). For each real number
be a transcendental entire function (cf. Entire function). For each real number 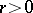 , let
, let 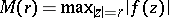 . Then the order of the transcendental entire function
. Then the order of the transcendental entire function 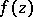 is defined as
is defined as
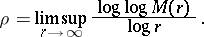 |
The function is called of finite order if 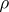 is finite and of infinite order otherwise.
is finite and of infinite order otherwise.
The order of an elliptic function is the number of times it takes each value in its period parallelogram, cf. Elliptic function.
Let 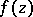 be a meromorphic function in
be a meromorphic function in 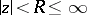 . For each possible value
. For each possible value 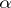 , including
, including 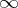 , let
, let
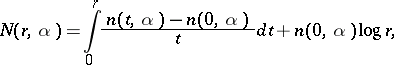 |
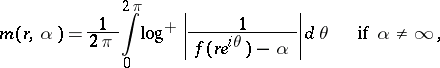 |
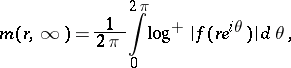 |
where 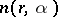 is the number of
is the number of 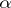 -points of
-points of 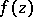 in
in 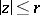 , i.e. the points with
, i.e. the points with 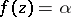 , counted with multiplicity. The functions
, counted with multiplicity. The functions 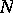 and
and 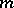 are called the counting function and proximity function, respectively. The function
are called the counting function and proximity function, respectively. The function 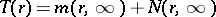 is called the order function or characteristic function of
is called the order function or characteristic function of 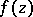 . One has
. One has 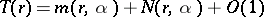 (Nevanlinna's first theorem), as
(Nevanlinna's first theorem), as  , for all
, for all 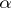 . One has also
. One has also
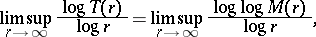 |
where, as in 16) above, 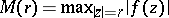 . The order of the meromorphic function
. The order of the meromorphic function 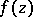 is defined as
is defined as 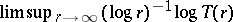 .
.
The 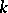 -th order modulus of continuity of a continuous function
-th order modulus of continuity of a continuous function 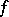 on
on 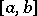 is defined by
is defined by
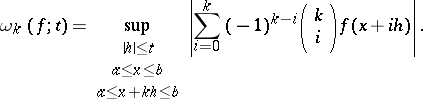 |
See also Continuity, modulus of; Smoothness, modulus of.
Consider a system of ordinary differential equations 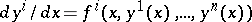 on an interval
on an interval 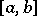 and a numerical solution method which calculates the
and a numerical solution method which calculates the 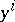 at mesh points
at mesh points 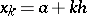 , so that
, so that 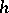 is the stepsize. Let
is the stepsize. Let 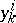 be the calculated value at
be the calculated value at 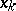 of
of 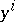 ,
, 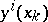 the "true value" ,
the "true value" , 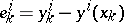 . If
. If 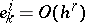 as
as 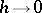 , then the solution process is of order
, then the solution process is of order  .
.
Consider an ordinary curve 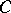 in
in  , i.e.
, i.e. 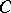 is the union of a finite number of simple arcs meeting at a finite number of points. For a point
is the union of a finite number of simple arcs meeting at a finite number of points. For a point 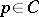 the boundary of a sufficiently small neighbourhood of
the boundary of a sufficiently small neighbourhood of 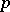 meets
meets  at a finite number of points, which is independent of the neighbourhood. This number is called the order of
at a finite number of points, which is independent of the neighbourhood. This number is called the order of 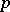 on
on 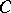 . A point of order 1 is an end point, one of order 2 an ordinary point, and one of order
. A point of order 1 is an end point, one of order 2 an ordinary point, and one of order 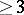 a branch point.
a branch point.
Let 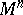 be an
be an  -dimensional manifold and
-dimensional manifold and 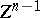 an
an 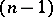 -dimensional cycle in
-dimensional cycle in 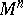 which is a boundary. The linking coefficient
which is a boundary. The linking coefficient 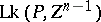 of a point
of a point 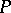 not in
not in 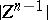 , the underlying space of
, the underlying space of 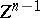 , with
, with  is called the order of the point
is called the order of the point 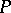 with respect to
with respect to 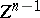 . In the case
. In the case 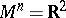 , and
, and 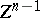 a closed curve
a closed curve 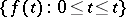 ,
, 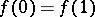 , this is the rotation number around
, this is the rotation number around 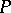 of
of 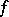 .
.
The word "order" also occurs as a synonym for an order relation on a set, or an ordering (cf. also Order (on a set)).
For the concept of order of magnitude of a function at a point (including 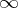 ) and related concepts cf. Order relation.
) and related concepts cf. Order relation.
Consider a Dirichlet series 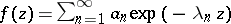 , and let
, and let 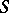 be the abscissa of convergence of
be the abscissa of convergence of 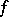 . I.e. the series converges for
. I.e. the series converges for 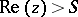 and diverges for
and diverges for 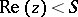 . If
. If 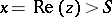 , then
, then  as
as 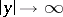 . In his thesis, H. Bohr introduced
. In his thesis, H. Bohr introduced
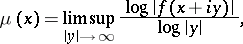 |
and called it the order of 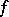 over the line
over the line 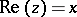 . The function
. The function 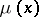 is non-negative, convex, continuous, and monotone decreasing. Bohr found that there is a kind of periodicity for the values of
is non-negative, convex, continuous, and monotone decreasing. Bohr found that there is a kind of periodicity for the values of 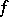 over this line; this started the theory of almost-periodic functions (cf. Almost-periodic function).
over this line; this started the theory of almost-periodic functions (cf. Almost-periodic function).
Let 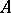 be a Dedekind domain, i.e. a (not necessarily commutative) integral domain in which every ideal is uniquely decomposed into prime ideals (cf. also Dedekind ring). Let
be a Dedekind domain, i.e. a (not necessarily commutative) integral domain in which every ideal is uniquely decomposed into prime ideals (cf. also Dedekind ring). Let 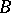 be a separable algebra of finite degree over
be a separable algebra of finite degree over 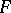 , the quotient field of
, the quotient field of 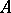 . An
. An 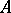 -lattice
-lattice 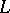 in
in 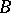 is a finitely-generated submodule (over
is a finitely-generated submodule (over 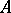 ) of
) of 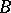 such that
such that 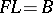 . An
. An 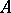 -lattice that is a subring of
-lattice that is a subring of 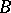 and which contains
and which contains  is called an
is called an 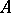 -order. A maximal order is one that is not contained in any order. Such a maximal order always exists. If
-order. A maximal order is one that is not contained in any order. Such a maximal order always exists. If 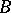 is commutative it is unique.
is commutative it is unique.
In the case 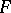 is a global or local field,
is a global or local field, 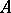 its ring of integers,
its ring of integers, 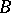 a finite field extension of
a finite field extension of 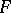 , the maximal order is the ring of integers of
, the maximal order is the ring of integers of  , which is the integral closure of
, which is the integral closure of 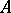 in
in 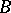 (cf. Integral extension of a ring). It is also called the principal order.
(cf. Integral extension of a ring). It is also called the principal order.
In some, mainly physics literature, one speaks of the order of a Lie group as the number of parameters needed to parametrize it, i.e. the order of the Lie group 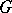 in this sense is the dimension of
in this sense is the dimension of 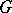 (cf. also Lie group).
(cf. also Lie group).
For references see the various articles directly or indirectly referred to.
Order. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Order&oldid=16876