Operator colligation
colligation of operators, node of operators, operator node
An aggregate of spaces and operators, to which is associated a characteristic operator-valued function. This characteristic function reflects properties of the colligation; for instance, multiplication of colligations results in multiplication of the corresponding characteristic functions. Colligations are used to build models for individual operators, but they are also employed in extension theory, interpolation theory, factorization problems, scattering theory, and system theory. They appear in different forms; the most frequently encountered forms are discussed below.
Let 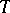 be a bounded linear mapping in a Hilbert space
be a bounded linear mapping in a Hilbert space 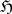 , and assume that the imaginary part
, and assume that the imaginary part 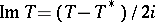 of
of 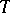 is represented as
is represented as 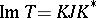 , where
, where 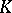 is a bounded linear mapping from a Hilbert space
is a bounded linear mapping from a Hilbert space  into
into 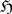 and
and 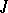 is a bounded, self-adjoint and unitary operator in
is a bounded, self-adjoint and unitary operator in 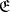 (cf. also Linear operator; Self-adjoint operator; Unitary operator). The aggregate of spaces and operators
(cf. also Linear operator; Self-adjoint operator; Unitary operator). The aggregate of spaces and operators
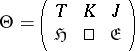 |
is called an operator colligation, and the corresponding operator-valued function 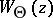 acting in
acting in  and defined by
and defined by
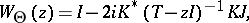 |
is called the characteristic operator-valued function of the colligation  . Clearly, the characteristic function satisfies the identity
. Clearly, the characteristic function satisfies the identity
 |
which exhibits many properties of 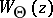 . The present notion of colligation is due to M.S. Brodskii and M.S. Livšic [a6], while the characteristic function was introduced, in a slightly different form, by Livšic in [a9]. The characteristic function is a unitary invariant of the non-self-adjoint operator
. The present notion of colligation is due to M.S. Brodskii and M.S. Livšic [a6], while the characteristic function was introduced, in a slightly different form, by Livšic in [a9]. The characteristic function is a unitary invariant of the non-self-adjoint operator 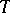 , and the singular points of this function coincide with the spectrum of the operator
, and the singular points of this function coincide with the spectrum of the operator  (cf. also Spectrum of an operator). The function
(cf. also Spectrum of an operator). The function 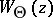 is a powerful tool for the investigation of the spectral properties of
is a powerful tool for the investigation of the spectral properties of 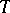 (invariant subspaces, triangular and functional models, Jordan representations, characterization of spectra, similarity), but it also plays a role in complex analysis (factorization into Blaschke–Potapov factors, interpolation problems); see [a3], [a17]. In system theory, the characteristic function is interpreted as the operator-valued transfer function of the system (conservative in the sense that
(invariant subspaces, triangular and functional models, Jordan representations, characterization of spectra, similarity), but it also plays a role in complex analysis (factorization into Blaschke–Potapov factors, interpolation problems); see [a3], [a17]. In system theory, the characteristic function is interpreted as the operator-valued transfer function of the system (conservative in the sense that  ) of the form
) of the form
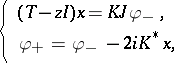 |
where 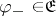 is an input vector,
is an input vector, 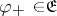 is an output vector and
is an output vector and  is a state space vector in
is a state space vector in 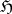 , so that
, so that 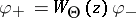 . The function
. The function 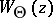 is determined through the imaginary part of the non-self-adjoint operator
is determined through the imaginary part of the non-self-adjoint operator 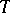 , and therefore this function is responsible for the spectral analysis of operators "close" to bounded self-adjoint operators.
, and therefore this function is responsible for the spectral analysis of operators "close" to bounded self-adjoint operators.
In the case where the operator 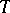 is unbounded, the Hilbert space
is unbounded, the Hilbert space  is assumed to be rigged, i.e. there exists a triplet of Hilbert spaces
is assumed to be rigged, i.e. there exists a triplet of Hilbert spaces  (cf. also Rigged Hilbert space). Let
(cf. also Rigged Hilbert space). Let  be a bounded linear operator from
be a bounded linear operator from 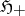 into
into 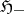 such that
such that 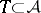 and
and 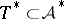 . In this case, assume that
. In this case, assume that 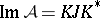 , where
, where 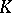 is a bounded linear operator from a Hilbert space
is a bounded linear operator from a Hilbert space  into
into 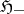 and
and 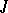 is a bounded, self-adjoint, and unitary operator in
is a bounded, self-adjoint, and unitary operator in 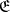 . Now the aggregate of spaces and operators
. Now the aggregate of spaces and operators
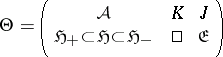 |
is called a rigged operator colligation and the corresponding characteristic function 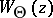 , acting in
, acting in  , is defined by
, is defined by
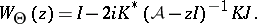 |
In this triplet setting, the system 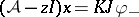 and
and 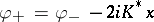 (conservative in the sense that
(conservative in the sense that 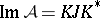 ) with an input vector
) with an input vector  , an output vector
, an output vector 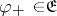 and a state space vector
and a state space vector 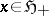 , leads to
, leads to 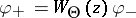 . Clearly, the definition for the unbounded case preserves the algebraic formalism developed for the bounded case. Rigged operator colligations and their characteristic operator-valued functions have been introduced by E.R. Tsekanovskii and Yu.L. Shmulyan [a18]. These types of colligations (with bounded or unbounded operator
. Clearly, the definition for the unbounded case preserves the algebraic formalism developed for the bounded case. Rigged operator colligations and their characteristic operator-valued functions have been introduced by E.R. Tsekanovskii and Yu.L. Shmulyan [a18]. These types of colligations (with bounded or unbounded operator 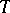 ) appear for instance in the theory of circuits, systems with distributed parameters and in scattering theory, see [a10], [a12]. Different definitions of characteristic functions (without colligations) for unbounded non-self-adjoint operators have been introduced and studied in [a8], [a15], [a16].
) appear for instance in the theory of circuits, systems with distributed parameters and in scattering theory, see [a10], [a12]. Different definitions of characteristic functions (without colligations) for unbounded non-self-adjoint operators have been introduced and studied in [a8], [a15], [a16].
The above colligations are associated to operators 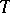 which are "close" to being self-adjoint. Similar notions can be developed for operators which are "close" to being unitary.
which are "close" to being self-adjoint. Similar notions can be developed for operators which are "close" to being unitary.
Let 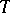 be a bounded operator in a Hilbert space
be a bounded operator in a Hilbert space 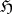 . Now, let
. Now, let 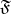 and
and 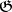 be Hilbert spaces, and let
be Hilbert spaces, and let 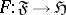 ,
, 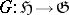 and
and 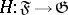 be bounded linear operators. The aggregate of spaces and operators
be bounded linear operators. The aggregate of spaces and operators
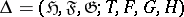 |
is called a unitary colligation if the operator matrix
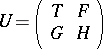 |
is a unitary operator from 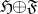 onto
onto  . The corresponding characteristic operator-valued function
. The corresponding characteristic operator-valued function 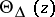 , acting from
, acting from 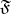 to
to 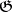 , is defined on the unit disc
, is defined on the unit disc  by
by
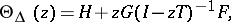 |
whose values are contractive inside 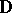 and unitary on the boundary of
and unitary on the boundary of 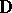 , as can be seen from identities such as
, as can be seen from identities such as
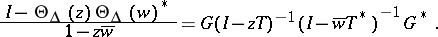 |
The operator 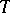 is called the main operator of the colligation
is called the main operator of the colligation 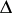 and it is a contraction. Conversely, any contraction
and it is a contraction. Conversely, any contraction  in
in 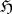 is the main operator of some unitary colligation, since the operator matrix
is the main operator of some unitary colligation, since the operator matrix
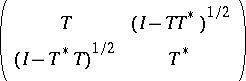 |
is unitary. The spectral theory of operators "close" to unitary operators has been developed by B. Sz.-Nagy and C. Foiaş [a13] through the characteristic functions of these augmented contractions. Later the theory was reformulated in terms of unitary operator colligations and their characteristic functions, see [a4]. The colligation  is called isometric, or co-isometric, if the operator matrix
is called isometric, or co-isometric, if the operator matrix  is isometric, respectively co-isometric. Unitary, isometric, or co-isometric colligations and their characteristic functions are being used in model theory [a19], [a14], and interpolation problems in Schur classes (cf. Schur functions in complex function theory); they also appear in extension theory, scattering theory and system theory [a2]. For instance, a discrete-time system of the form
is isometric, respectively co-isometric. Unitary, isometric, or co-isometric colligations and their characteristic functions are being used in model theory [a19], [a14], and interpolation problems in Schur classes (cf. Schur functions in complex function theory); they also appear in extension theory, scattering theory and system theory [a2]. For instance, a discrete-time system of the form
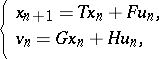 |
with 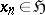 ,
, 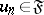 and
and 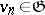 ,
, 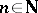 , is called conservative if the corresponding operator colligation
, is called conservative if the corresponding operator colligation 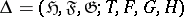 is unitary. Solving this system by means of
is unitary. Solving this system by means of  ,
,  and
and 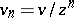 , with
, with  ,
, 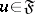 ,
, 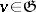 , and
, and 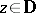 , leads to
, leads to 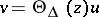 .
.
In all types of colligations questions arise concerning the dimension of the state space 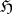 and the minimality of the representation. Likewise, there are various constructions to build state spaces by means of characteristic functions (model theory). Operator colligations have been considered in the setting of Banach spaces [a5] and in the setting of indefinite inner product spaces (see for instance [a1] for Pontryagin spaces (cf. also Pontryagin space), and [a1], p. 205, for references for the case of Krein spaces, cf. also Krein space). Recently (1999) there is interest in colligations associated with commuting operators [a11] and in colligations with several variables [a7].
and the minimality of the representation. Likewise, there are various constructions to build state spaces by means of characteristic functions (model theory). Operator colligations have been considered in the setting of Banach spaces [a5] and in the setting of indefinite inner product spaces (see for instance [a1] for Pontryagin spaces (cf. also Pontryagin space), and [a1], p. 205, for references for the case of Krein spaces, cf. also Krein space). Recently (1999) there is interest in colligations associated with commuting operators [a11] and in colligations with several variables [a7].
References
| [a1] | D. Alpay, A. Dijksma, J. Rovnyak, H.S.V. de Snoo, "Schur functions, operator colligations, and reproducing kernel Pontryagin spaces" , Oper. Th. Adv. Appl. , 96 , Birkhäuser (1997) |
| [a2] | D.Z. Arov, L.Z. Grossman, "Scattering matrices in the theory of extensions of isometric operators" Math. Nachr. , 157 (1992) pp. 105–123 |
| [a3] | M.S. Brodskii, "Triangular and Jordan representations of linear operators" , Transl. Math. Monographs , 32 , Amer. Math. Soc. (1971) (In Russian) |
| [a4] | M.S. Brodskii, "Unitary operator colligations and their characteristic functions" Russian Math. Surveys , 33 : 4 (1978) pp. 159–191 Uspekhi Mat. Nauk. , 33 : 4 (202) (1978) pp. 141–168 |
| [a5] | H. Bart, I. Gohberg, M.A. Kaashoek, "Minimal factorization of matrix and operator functions" , Oper. Th. Adv. Appl. , 1 , Birkhäuser (1979) |
| [a6] | M.S. Brodskii, M.S. Livšic, "Spectral analysis of non-selfadjoint operators and intermediate systems" Amer. Math. Soc. Transl. , 13 : 2 (1960) pp. 265–346 Uspekhi Mat. Nauk. , 13 : 1 (79) (1958) pp. 3–85 |
| [a7] | J.A. Ball, T.T. Trent, "Unitary colligations, reproducing kernel Hilbert spaces, and Nevanlinna–Pick interpolation in several variables" J. Funct. Anal. , 157 (1998) pp. 1–61 |
| [a8] | A. Kuzhel, "Characteristic functions and models of nonselfadjoint operators" , Kluwer Acad. Publ. (1996) |
| [a9] | M.S. Livšic, "On the spectral decomposition of linear non-selfadjoint operators" Amer. Math. Soc. Transl. , 5 : 2 (1957) pp. 67–114 Mat. Sb. , 34 : 76 (1954) pp. 145–199 |
| [a10] | M.S. Livšic, "Operators, oscillations, waves" , Transl. Math. Monographs , 34 , Amer. Math. Soc. (1973) (In Russian) |
| [a11] | M.S. Livšic, N. Kravitsky, A.S. Markus, V. Vinnikov, "Theory of commuting nonselfadjoint operators" , Kluwer Acad. Publ. (1995) |
| [a12] | M.S. Livšic, A.A. Yantsevich, "Operator colligations in Hilbert spaces" , Winston (1979) (In Russian) |
| [a13] | B. Sz.-Nagy, C. Foiaş, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) |
| [a14] | N. Nikolski, V. Vasyunin, "Elements of spectral theory in terms of the free function model I. Basic constructions" , Holomorphic spaces (Berkeley, CA, 1995) , Cambridge Univ. Press (1998) pp. 211–302 |
| [a15] | B.S. Pavlov, "Spectral analysis of a singular Schrödinger operator in terms of a functional model" , Partial Differential Equations VIII , Springer (1995) pp. 89–153 |
| [a16] | A.V. Štrauss, "Characteristic functions of linear operators" Amer. Math. Soc. Transl. , 40 : 2 (1964) pp. 1–37 Izv. Akad. Nauk. SSSR Ser. Mat. , 24 (1960) pp. 43–74 |
| [a17] | L.A. Sakhnovich, "Interpolation theory and its applications" , Kluwer Acad. Publ. (1997) |
| [a18] | E.R. Tsekanovskii, Yu.L. Shmulyan, "The theory of bi-extensions of operators on rigged Hilbert spaces. Unbounded operator colligations and characteristic functions" Russian Math. Surveys , 32 : 5 (1977) pp. 73–131 Uspekhi Mat. Nauk. , 32 : 5 (1977) pp. 69–124 |
| [a19] | L. de Branges, J. Rovnyak, "Square summable power series" , Holt, Rinehart & Winston (1966) |
Operator colligation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator_colligation&oldid=12813