One-sided limit
The limit of a function at a point from the right or left. Let  be a mapping from an ordered set
be a mapping from an ordered set 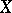 (for example, a set lying in the real line), regarded as a topological space with the topology generated by the order relation, into a topological space
(for example, a set lying in the real line), regarded as a topological space with the topology generated by the order relation, into a topological space 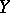 , and let
, and let 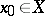 . The limit of
. The limit of 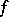 with respect to any interval
with respect to any interval 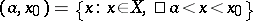 is called the limit of
is called the limit of 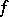 on the left, and is denoted by
on the left, and is denoted by
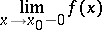 |
(it does not depend on the choice of  ), and the limit with respect to the interval
), and the limit with respect to the interval 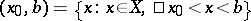 is called the limit on the right, and is denoted by
is called the limit on the right, and is denoted by
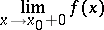 |
(it does not depend on the choice of 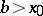 ). If the point
). If the point 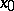 is a limit point both on the left and the right for the domain of definition of the function
is a limit point both on the left and the right for the domain of definition of the function 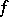 , then the usual limit
, then the usual limit
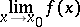 |
with respect to a deleted neighbourhood of 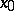 (in this case it is also called a two-sided limit, in contrast to the one-sided limits) exists if and only if both of the left and right one-sided limits exist at
(in this case it is also called a two-sided limit, in contrast to the one-sided limits) exists if and only if both of the left and right one-sided limits exist at 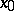 and they are equal.
and they are equal.
Comments
Instead of 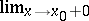 (respectively,
(respectively, 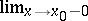 ) one also finds the notations
) one also finds the notations 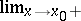 ,
, 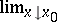 (respectively,
(respectively, 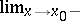 ,
, 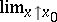 ).
).
One-sided limit. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=One-sided_limit&oldid=19010