Omega-squared distribution
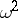 -distribution
-distribution
The probability distribution of the random variable
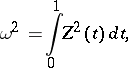 |
where 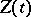 is a conditional Wiener process (conditioned on
is a conditional Wiener process (conditioned on 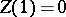 ). The characteristic function of the "omega-squared" distribution is expressed by the formula
). The characteristic function of the "omega-squared" distribution is expressed by the formula
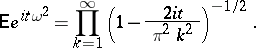 |
In mathematical statistics, the "omega-squared" distribution is often found in the following circumstances. Let 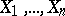 be independent random variables, uniformly distributed on
be independent random variables, uniformly distributed on 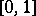 , according to which an empirical distribution function
, according to which an empirical distribution function 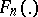 is constructed. In this case, the process
is constructed. In this case, the process
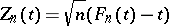 |
converges weakly to a conditional Wiener process, from which it follows that
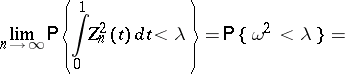 |
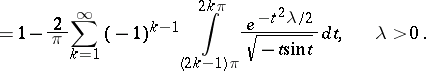 |
See also Cramér–von Mises test.
References
| [1] | N.V. Smirnov, "On the 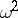 -distribution" Mat. Sb. , 2 (1937) pp. 973–993 (In Russian) -distribution" Mat. Sb. , 2 (1937) pp. 973–993 (In Russian) |
| [2] | T.W. Anderson, D.A. Darling, "Asymptotic theory of certain "goodness of fit" criteria based on stochastic processes" Ann. Math. Stat. , 23 (1952) pp. 193–212 |
Comments
The "conditional Wiener process" 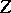 is usually referred to in the Western literature as tied-down Brownian motion, pinned Brownian motion or as the Brownian bridge.
is usually referred to in the Western literature as tied-down Brownian motion, pinned Brownian motion or as the Brownian bridge.
The pioneering paper is [a1].
References
| [a1] | D.A. Darling, "The Cramér–Smirnov test in the parametric case" Ann. Math. Stat. , 26 (1955) pp. 1–20 |
| [a2] | J. Durbin, "Distribution theory for tests based on the sample distribution function" , SIAM (1973) |
Omega-squared distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Omega-squared_distribution&oldid=17313