Oka theorems
Theorems on the classical problems in the theory of functions of several complex variables, first proved by K. Oka between 1930 and 1950 (see [1]).
1) Oka's theorem on the Cousin problems: The first Cousin problem is solvable in any domain of holomorphy in 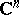 ; the second Cousin problem is solvable in any domain of holomorphy
; the second Cousin problem is solvable in any domain of holomorphy  that is homeomorphic to
that is homeomorphic to 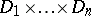 , where all domains
, where all domains 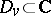 , except for, possibly, one, are simply connected.
, except for, possibly, one, are simply connected.
2) Oka's theorem on the Levi problem: Any pseudo-convex Riemannian domain (cf. Pseudo-convex and pseudo-concave) is a domain of holomorphy.
Originally Oka proved these theorems in dimension 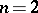 ; in the case of arbitrary dimension, the theorems were also proved by other mathematicians.
; in the case of arbitrary dimension, the theorems were also proved by other mathematicians.
3) The Oka–Weil theorem: Let 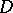 be a domain in
be a domain in 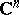 and let the compact set
and let the compact set 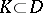 coincide with its hull with respect to the algebra
coincide with its hull with respect to the algebra  of all functions holomorphic in
of all functions holomorphic in 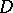 (cf. Holomorphic envelope); then for any function
(cf. Holomorphic envelope); then for any function 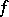 holomorphic in a neighbourhood of
holomorphic in a neighbourhood of  , and for any
, and for any 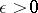 , a function
, a function 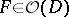 can be found such that
can be found such that
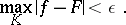 |
This fundamental theorem in the theory of holomorphic approximation is extensively used in complex and functional analysis.
4) Oka's coherence theorem: Let 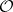 be a sheaf of holomorphic functions on a complex manifold
be a sheaf of holomorphic functions on a complex manifold 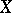 ; then for any natural number
; then for any natural number 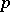 , any locally finitely-generated subsheaf of the sheaf
, any locally finitely-generated subsheaf of the sheaf 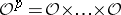 (
(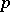 times) is a coherent analytic sheaf (cf. Coherent sheaf).
times) is a coherent analytic sheaf (cf. Coherent sheaf).
This is one of the basic theorems of the so-called Oka–Cartan theory, which is used essentially in proving the Cartan theorems 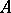 and
and 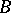 (cf. Cartan theorem).
(cf. Cartan theorem).
References
| [1] | K. Oka, "Sur les fonctions analytiques de plusieurs variables" , Iwanami Shoten (1961) |
| [2] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) |
| [3] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
Comments
Reference [a2] is an annotated English translation of Oka's fundamental papers.
References
| [a1] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) |
| [a2] | K. Oka, "Collected papers" , Springer (1984) |
| [a3] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. 1, Sect. 3 |
Oka theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oka_theorems&oldid=19092