Difference between revisions of "Odlyzko bounds"
(Importing text file) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 28 formulas, 26 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
| + | Effective lower bounds for $M ( r _ { 1 } , r _ { 2 } )$, the minimal value of the [[Discriminant|discriminant]] $| d ( K ) |$ of algebraic number fields $K$ having signature $( r _ { 1 } , r _ { 2 } )$ (i.e. having $r_1$ real and $2r_2$ non-real conjugates), obtained in 1976 by A.M. Odlyzko. See also [[Algebraic number|Algebraic number]]; [[Number field|Number field]]. | ||
The first such bound was proved in 1891 by H. Minkowski [[#References|[a4]]], who showed | The first such bound was proved in 1891 by H. Minkowski [[#References|[a4]]], who showed | ||
| − | + | \begin{equation} \tag{a1} M ( r _ { 1 } , r _ { 2 } ) > \left( \frac { \pi } { 4 } \right) ^ { 2 r _ { 2 } } \left( \frac { n ^ { n } } { n ! } \right) ^ { 2 }, \end{equation} | |
| − | with | + | with $n = r _ { 1 } + 2 r _ { 2 }$. He obtained it using methods from the [[Geometry of numbers|geometry of numbers]]; the same method was used later by several authors to improve (a1) (see [[#References|[a5]]] for the strongest result obtained in this way). |
| − | In 1974, H.M. Stark ([[#References|[a11]]], [[#References|[a12]]]) observed that Hadamard factorization of the [[Dedekind zeta-function|Dedekind zeta-function]] | + | In 1974, H.M. Stark ([[#References|[a11]]], [[#References|[a12]]]) observed that Hadamard factorization of the [[Dedekind zeta-function|Dedekind zeta-function]] $\zeta _ { K } ( s )$ leads to a formula expressing $\operatorname{log} | d ( K ) |$ by the zeros of $\zeta _ { K } ( s )$ and the value of its logarithmic derivative at a complex number $s _ { 0 } \neq 0,1$ with $\zeta_{ K } ( s _ { 0 } ) \neq 0$. He used this formula with a proper choice of $s_0$ to deduce lower bounds for $M ( r _ { 1 } , r _ { 2 } )$ which were essentially stronger than Minkowski's bound, but did not reach the bounds obtained by geometrical methods. |
In 1976, Odlyzko [[#References|[a7]]] (cf. [[#References|[a9]]]) modified Stark's formula and obtained the following important improvement of (a1): | In 1976, Odlyzko [[#References|[a7]]] (cf. [[#References|[a9]]]) modified Stark's formula and obtained the following important improvement of (a1): | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o130/o130020/o13002016.png"/></td> <td style="width:5%;text-align:right;" valign="top">(a2)</td></tr></table> |
| − | with | + | with $\operatorname { lim } _ { x \rightarrow \infty } \epsilon ( n ) = 0$. |
In particular, one has | In particular, one has | ||
| − | + | \begin{equation*} D = \liminf _ { n \rightarrow \infty } M ( r _ { 1 } , r _ { 2 } ) ^ { 1 / n } \geq 22. \end{equation*} | |
| − | If the extended Riemann hypothesis is assumed (cf. also [[Riemann hypotheses|Riemann hypotheses]]; [[Zeta-function|Zeta-function]]), then the constants | + | If the extended Riemann hypothesis is assumed (cf. also [[Riemann hypotheses|Riemann hypotheses]]; [[Zeta-function|Zeta-function]]), then the constants $60$ and $22$ in (a2) can be replaced by $180$ and $41$, respectively. For small degrees the bound (a2) can be improved (see [[#References|[a2]]], [[#References|[a10]]]) and several exact values of $M ( r _ { 1 } , r _ { 2 } )$ are known. |
| − | On the other hand, it has been shown in [[#References|[a13]]], as a consequence of their solution of the class field tower problem (cf. also [[Tower of fields|Tower of fields]]; [[Class field theory|Class field theory]]), that | + | On the other hand, it has been shown in [[#References|[a13]]], as a consequence of their solution of the class field tower problem (cf. also [[Tower of fields|Tower of fields]]; [[Class field theory|Class field theory]]), that $D$ is finite. The best explicit upper bound for it, $D \leq 92.4$, is due to J. Martinet [[#References|[a1]]], who obtained this as a corollary of his constructions of infinite $2$-class towers of suitable fields. |
For surveys of this topic, see [[#References|[a9]]], [[#References|[a3]]] and [[#References|[a8]]]. | For surveys of this topic, see [[#References|[a9]]], [[#References|[a3]]] and [[#References|[a8]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J. Martinet, "Tours de corps de classes et estimations de discriminants" ''Invent. Math.'' , '''44''' (1978) pp. 65–73</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J. Martinet, "Petits discriminants" ''Ann. Inst. Fourier (Grenoble)'' , '''29''' : fasc.1 (1979) pp. 159–170</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J. Martinet, "Petits discriminants des corps de nombres" , ''Journ. Arithm. 1980'' , Cambridge Univ. Press (1982) pp. 151–193</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> H. Minkowski, "Théorèmes arithmétiques" ''C.R. Acad. Sci. Paris'' , '''112''' (1891) pp. 209–212 (Gesammelte Abh. I (1911), 261-263, Leipzig–Berlin)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> H.P. Mulholland, "On the product of $n$ complex homogeneous linear forms" ''J. London Math. Soc.'' , '''35''' (1960) pp. 241–250</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> A. Odlyzko, "Some analytic estimates of class numbers and discriminants" ''Invent. Math.'' , '''29''' (1975) pp. 275–286</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> A. Odlyzko, "Lower bounds for discriminants of number fields" ''Acta Arith.'' , '''29''' (1976) pp. 275–297 (II: Tôhoku Math. J., 29 (1977), 275-286)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> A. Odlyzko, "Bounds for discriminants and related estimates for class numbers, regulators and zeros of zeta functions: a survey of recent results" ''Sém. de Théorie des Nombres, Bordeaux'' , '''2''' (1990) pp. 119–141</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> G. Poitou, "Minoration de discriminants (d'aprés A.M. Odlyzko)" , ''Sém. Bourbaki (1975/76)'' , ''Lecture Notes in Mathematics'' , '''567''' , Springer (1977) pp. 136–153</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> G. Poitou, "Sur les petits discriminants" ''Sém. Delange–Pisot–Poitou'' , '''18''' : 6 (1976/77)</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> H.M. Stark, "Some effective cases of the Brauer–Siegel theorem" ''Invent. Math.'' , '''23''' (1974) pp. 135–152</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> H.M. Stark, "The analytic theory of numbers" ''Bull. Amer. Math. Soc.'' , '''81''' (1975) pp. 961–972,</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> E.S. Golod, I.R. Shafarevich, "On the class-field tower" ''Izv. Akad. Nauk. SSSR'' , '''28''' (1964) pp. 261–272 (In Russian)</td></tr></table> |
Revision as of 17:45, 1 July 2020
Effective lower bounds for $M ( r _ { 1 } , r _ { 2 } )$, the minimal value of the discriminant $| d ( K ) |$ of algebraic number fields $K$ having signature $( r _ { 1 } , r _ { 2 } )$ (i.e. having $r_1$ real and $2r_2$ non-real conjugates), obtained in 1976 by A.M. Odlyzko. See also Algebraic number; Number field.
The first such bound was proved in 1891 by H. Minkowski [a4], who showed
\begin{equation} \tag{a1} M ( r _ { 1 } , r _ { 2 } ) > \left( \frac { \pi } { 4 } \right) ^ { 2 r _ { 2 } } \left( \frac { n ^ { n } } { n ! } \right) ^ { 2 }, \end{equation}
with $n = r _ { 1 } + 2 r _ { 2 }$. He obtained it using methods from the geometry of numbers; the same method was used later by several authors to improve (a1) (see [a5] for the strongest result obtained in this way).
In 1974, H.M. Stark ([a11], [a12]) observed that Hadamard factorization of the Dedekind zeta-function $\zeta _ { K } ( s )$ leads to a formula expressing $\operatorname{log} | d ( K ) |$ by the zeros of $\zeta _ { K } ( s )$ and the value of its logarithmic derivative at a complex number $s _ { 0 } \neq 0,1$ with $\zeta_{ K } ( s _ { 0 } ) \neq 0$. He used this formula with a proper choice of $s_0$ to deduce lower bounds for $M ( r _ { 1 } , r _ { 2 } )$ which were essentially stronger than Minkowski's bound, but did not reach the bounds obtained by geometrical methods.
In 1976, Odlyzko [a7] (cf. [a9]) modified Stark's formula and obtained the following important improvement of (a1):
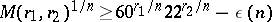 | (a2) |
with $\operatorname { lim } _ { x \rightarrow \infty } \epsilon ( n ) = 0$.
In particular, one has
\begin{equation*} D = \liminf _ { n \rightarrow \infty } M ( r _ { 1 } , r _ { 2 } ) ^ { 1 / n } \geq 22. \end{equation*}
If the extended Riemann hypothesis is assumed (cf. also Riemann hypotheses; Zeta-function), then the constants $60$ and $22$ in (a2) can be replaced by $180$ and $41$, respectively. For small degrees the bound (a2) can be improved (see [a2], [a10]) and several exact values of $M ( r _ { 1 } , r _ { 2 } )$ are known.
On the other hand, it has been shown in [a13], as a consequence of their solution of the class field tower problem (cf. also Tower of fields; Class field theory), that $D$ is finite. The best explicit upper bound for it, $D \leq 92.4$, is due to J. Martinet [a1], who obtained this as a corollary of his constructions of infinite $2$-class towers of suitable fields.
For surveys of this topic, see [a9], [a3] and [a8].
References
| [a1] | J. Martinet, "Tours de corps de classes et estimations de discriminants" Invent. Math. , 44 (1978) pp. 65–73 |
| [a2] | J. Martinet, "Petits discriminants" Ann. Inst. Fourier (Grenoble) , 29 : fasc.1 (1979) pp. 159–170 |
| [a3] | J. Martinet, "Petits discriminants des corps de nombres" , Journ. Arithm. 1980 , Cambridge Univ. Press (1982) pp. 151–193 |
| [a4] | H. Minkowski, "Théorèmes arithmétiques" C.R. Acad. Sci. Paris , 112 (1891) pp. 209–212 (Gesammelte Abh. I (1911), 261-263, Leipzig–Berlin) |
| [a5] | H.P. Mulholland, "On the product of $n$ complex homogeneous linear forms" J. London Math. Soc. , 35 (1960) pp. 241–250 |
| [a6] | A. Odlyzko, "Some analytic estimates of class numbers and discriminants" Invent. Math. , 29 (1975) pp. 275–286 |
| [a7] | A. Odlyzko, "Lower bounds for discriminants of number fields" Acta Arith. , 29 (1976) pp. 275–297 (II: Tôhoku Math. J., 29 (1977), 275-286) |
| [a8] | A. Odlyzko, "Bounds for discriminants and related estimates for class numbers, regulators and zeros of zeta functions: a survey of recent results" Sém. de Théorie des Nombres, Bordeaux , 2 (1990) pp. 119–141 |
| [a9] | G. Poitou, "Minoration de discriminants (d'aprés A.M. Odlyzko)" , Sém. Bourbaki (1975/76) , Lecture Notes in Mathematics , 567 , Springer (1977) pp. 136–153 |
| [a10] | G. Poitou, "Sur les petits discriminants" Sém. Delange–Pisot–Poitou , 18 : 6 (1976/77) |
| [a11] | H.M. Stark, "Some effective cases of the Brauer–Siegel theorem" Invent. Math. , 23 (1974) pp. 135–152 |
| [a12] | H.M. Stark, "The analytic theory of numbers" Bull. Amer. Math. Soc. , 81 (1975) pp. 961–972, |
| [a13] | E.S. Golod, I.R. Shafarevich, "On the class-field tower" Izv. Akad. Nauk. SSSR , 28 (1964) pp. 261–272 (In Russian) |
Odlyzko bounds. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Odlyzko_bounds&oldid=15182