Octacode
Led by modulation considerations, G.D. Forney and M.D. Trott discovered in October 1992 that the Nordstrom–Robinson code was obtained by Gray mapping (cf. also Gray code) a certain  code of length
code of length  and minimum Lee distance
and minimum Lee distance  Seeing the parity-check matrix of that code,
Seeing the parity-check matrix of that code,
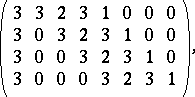 |
NJ.A. Sloane identified this code with the octacode [a4], which had turned up already in one of the "holy constructions" of the Leech lattice [a2], Chapt. 24, in particular in the construction based on  . The Leech lattice, the conjecturally densest sphere packing in
. The Leech lattice, the conjecturally densest sphere packing in  dimensions, can be built up from a product of eight copies of the face-centred cubic lattice
dimensions, can be built up from a product of eight copies of the face-centred cubic lattice  , the conjecturally densest sphere packing in three dimensions. The quotient of
, the conjecturally densest sphere packing in three dimensions. The quotient of  in its dual lattice
in its dual lattice 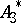 is a cyclic group of order
is a cyclic group of order  , and so to get the Leech lattice from
, and so to get the Leech lattice from  one needs a code of length
one needs a code of length 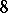 over
over 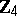 .
.
The preceding matrix shows that the octacode is an extended cyclic code with parity-check polynomial  , which reduced modulo
, which reduced modulo  yields
yields  , which is the generator matrix of the
, which is the generator matrix of the 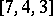 binary Hamming code. It is indeed both the first quaternary Kerdock code and the first quaternary Preparata code [a5] (cf. also Kerdock and Preparata codes), and as such it is self-dual [a3]. It is indeed of type II, i.e. the Euclidean weight of its words is multiple of
binary Hamming code. It is indeed both the first quaternary Kerdock code and the first quaternary Preparata code [a5] (cf. also Kerdock and Preparata codes), and as such it is self-dual [a3]. It is indeed of type II, i.e. the Euclidean weight of its words is multiple of 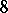 ; the attached lattice is
; the attached lattice is 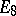 , the unique even unimodular lattice in dimension
, the unique even unimodular lattice in dimension  [a1]. Its residue code modulo
[a1]. Its residue code modulo  is the doubly even binary self-dual code
is the doubly even binary self-dual code  .
.
References
| [a1] | A. Bonnecaze, P. Solé, A.R. Calderbank, "Quaternary construction of unimodular lattices" IEEE Inform. Th. , 41 (1995) pp. 366–376 |
| [a2] | J.H. Conway, N.J.A. Sloane, "Sphere packings, lattices and groups" , Springer (1992) |
| [a3] | J.H. Conway, N.J.A. Sloane, "Self-dual codes over the integers modulo 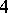 " J. Combin. Th. A , 62 (1993) pp. 31–45 " J. Combin. Th. A , 62 (1993) pp. 31–45 |
| [a4] | G.D. Forney, N.J.A. Sloane, M.D. Trott, "The Nordstrom Robinson code is the binary image of the octacode" R. Calderbank (ed.) G.D. Forney Jr. (ed.) N. Moayeri (ed.) , Coding and Quantization , Amer. Math. Soc. (1993) pp. 19–26 |
| [a5] | A.R. Hammons, P.V. Kumar, A.R. Calderbank, N.J.A. Sloane, P. Solé, "The 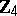 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 |
Octacode. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Octacode&oldid=12845