Obstruction

A concept in homotopy theory: An invariant that equals zero if a (step in a) corresponding problem is solvable and is non-zero otherwise.

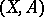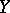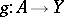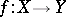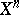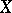Let be a pair of cellular spaces (cf. Cellular space) and let be a simply-connected (more generally, a homotopy-simple) topological space. Can one extend a given continuous mapping to a continuous mapping ? The extension can be attempted recursively, over successive skeletons of . Suppose one has constructed a mapping 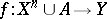such that 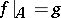. For any oriented 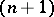-dimensional cell 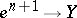the mapping 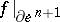gives a mapping 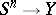(where 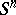is the -dimensional unit sphere) and an element 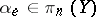(it is here that one uses that 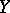is homotopy simple, which allows one to ignore the base point). This defines a cochain

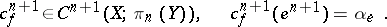Since for 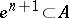one clearly has 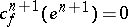, it follows that

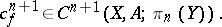Clearly 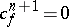if and only if 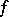can be extended to 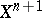, i.e. 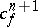is an obstruction to extending 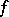to .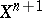

The cochain 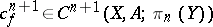is a cocycle. The fact that 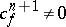does not, in general, imply that 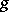cannot be extended to 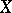: It is possible that 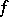cannot be extended to 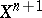because of an unsuccessful choice of an extension of 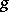to 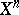. It may turn out that, e.g., the mapping 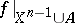can be extended to 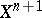, i.e. that extension is possible by skipping back one step. It can be shown that the cohomology class

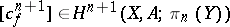is an obstruction to this, i.e. 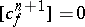if and only if there is a mapping 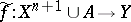such that 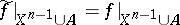(in particular, 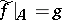). The construction of difference chains and cochains is used in the proof of this statement (cf. Difference cochain and chain).

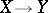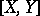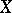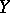Since the problem of homotopy classification of mappings can be interpreted as an extension problem, obstruction theory is applicable also to the description of the set of homotopy classes of mappings from into . Let 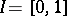and let 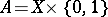be a subspace of 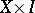. Then a pair of mappings 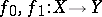is interpreted as a mapping 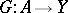, , 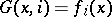, 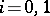and the presence of a homotopy between 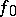and 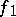means the presence of a mapping 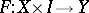extending 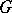. If the homotopy 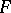has been constructed on the -dimensional skeleton of 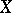, then the obstruction to its extension to 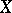is the difference cochain

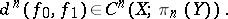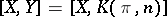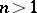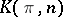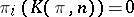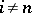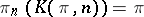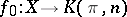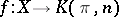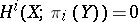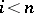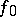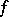As an application one may consider the description of the set , , where is the Eilenberg–MacLane space: for ; . Let be a constant mapping and an arbitrary continuous mapping. Since for , the mappings and are homotopic on 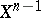and, after having chosen such a homotopy, one can define the difference cochain

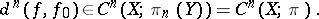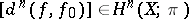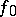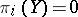The cohomology class is well-defined, i.e. does not depend on the choice of a homotopy between and (since for 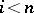). Further, if two mappings 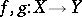are such that 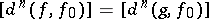, then 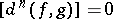, and hence 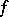and 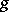are homotopic on 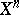. The obstructions to extending this homotopy to 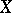lie in the groups (since 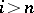), and hence 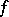and 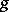are homotopic. Thus, the homotopy class of 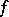is completely determined by the element 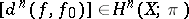. Finally, for any 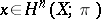there is a mapping 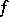with 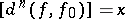, hence 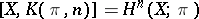. Similarly, if 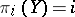for 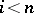and if 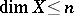, then .

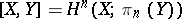In studying extension problems one has considered the possibility of extending "by skipping back one step" . A complete solution of the problem requires the analysis of the possibility of skipping back an arbitrary number of steps. Cohomology operations (cf. Cohomology operation) and Postnikov systems (cf. Postnikov system) are used to this end. E.g., in order to describe the set 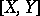, where 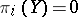for 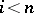, , 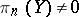, 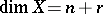it is required, in general, to study the possibility of skipping back 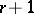steps, for which it is necessary to study the first 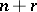levels of the Postnikov system for 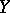, i.e. to use cohomology operations of orders 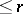(in the article Cohomology operation this problem is outlined for ).

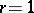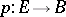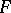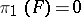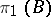The theory of obstructions is also used in the more general situation of extension of sections (cf. Section of a mapping). Let be a fibration with fibre (where and acts trivially on 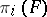), let 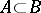and let be a section (i.e. a continuous mapping such that 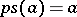). Can one extend to 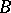? The corresponding obstructions lie in the groups 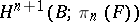. An extension problem is obtained from this problem if one puts 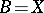, , 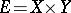, 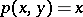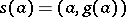. Analogously one can also study the classification problem for sections using obstruction theory.

Finally, one can remove the restriction of homotopic simplicity of the space 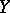in the extension problem (as well as in the problem on sections); then one must use cohomology with local coefficients.

Obstruction theory was initiated by S. Eilenberg [2]. It was also known to L.S. Pontryagin, who did not formulate it explicitly but used it for the solution of concrete problems, see [1].

A good discussion can be found in [3] and [4].

References

[1]	L.S. Pontryagin, "Classification of continuous transformations of a complex into a sphere" Dokl. Akad. Nauk SSSR , 19 (1938) pp. 361–363 (In Russian)
[2]	S. Eilenberg, "Cohomology and continuous mappings" Ann. of Math. , 41 (1940) pp. 231–251
[3]	S.-T. Hu, "Homotopy theory" , Acad. Press (1959)
[4]	E. Thomas, "Seminar on fibre spaces" , Springer (1966)

Comments

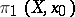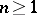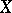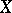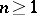The fundamental group acts on the homotopy groups , , cf. Homotopy group. The space is called -simple if this action (for this ) is trivial; is called simple or homotopy simple if it is path connected and -simple for all . Then 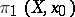is Abelian and acts trivially on all 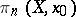. A path-connected 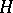-space is simple.

References

[a1]	N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951)
[a2]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. 269–276; 429–432
[a3]	G.W. Whitehead, "Elements of homotopy theory" , Springer (1978)
[a4]	H.J. Baues, "Obstruction theory" , Springer (1977)