Oberbeck-Boussinesq equations
Equations giving an approximate description of the thermo-mechanical response of linearly viscous fluids (Navier–Stokes fluids or Newtonian fluids) that can only sustain volume-preserving motions (isochoric motions) in isothermal processes, but can undergo motions that are not volume-preserving during non-isothermal processes. Such a restriction on the response of the fluid requires that the determinant of the deformation gradient 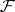 be a function of the temperature
be a function of the temperature 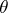 , i.e.,
, i.e.,
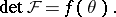 | (a1) |
An approximation of the balance of mass, momentum and energy within the context of the above constraint was first discussed by A. Oberbeck [a1] and later by J. Boussinesq [a2]. Such an approximate system has relevance to a plethora of problems in astrophysics, geophysics and oceanography.
Numerous attempts have been made to provide a rigorous justification for the Oberbeck–Boussinesq equations, the details of which can be found in [a3].
While plausible arguments based on physical grounds are advanced to derive the Oberbeck–Boussinesq equations (see [a4]), namely that the effects of the variations in the density with respect to the temperature are more significant in the buoyancy forces than in the inertial effects, no compelling evidence or a rigorous mathematical basis is available.
The constraint (a1) implies that
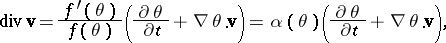 |
where  is the velocity field,
is the velocity field, 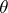 the temperature, and
the temperature, and 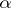 the coefficient of thermal expansion.
the coefficient of thermal expansion.
Thus, while in an incompressible fluid
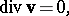 | (a2) |
this is not necessarily so for fluids obeying (a1). However, in the Oberbeck–Boussinesq equations the constraint (a2) holds to within the order of approximation.
Let 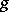 denote the acceleration due to gravity, let
denote the acceleration due to gravity, let 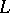 be a typical length scale (usually the thickness of the layer of the fluid),
be a typical length scale (usually the thickness of the layer of the fluid), 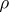 a representative density,
a representative density, 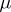 the viscosity, and
the viscosity, and 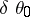 a characteristic temperature difference. Assume that
a characteristic temperature difference. Assume that 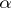 is a constant. On introducing a characteristic velocity
is a constant. On introducing a characteristic velocity 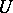 and characteristic time
and characteristic time 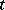 for the problem through (see [a4])
for the problem through (see [a4])
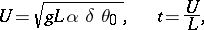 |
one can set the relevant non-dimensional parameters to be
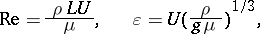 |
where 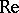 is called the Reynolds number.
is called the Reynolds number.
Assuming that 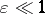 and
and 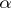 is a constant, and expressing the (non-dimensional) velocity
is a constant, and expressing the (non-dimensional) velocity  , the temperature
, the temperature 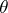 and the pressure
and the pressure 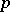 through
through
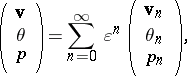 |
and substituting the above into the governing equations for mass, momentum and energy balance for a Navier–Stokes fluid leads to an hierarchy of equations at different orders of  . Let
. Let 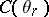 denote the specific heat at some reference temperature
denote the specific heat at some reference temperature  and set
and set 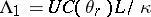 ,
, 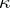 being the thermal conductivity. Let
being the thermal conductivity. Let 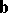 denote the field of the body forces. Then the equations at
denote the field of the body forces. Then the equations at 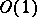 read
read
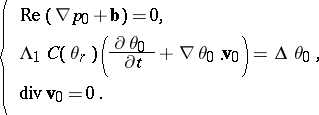 | (a3) |
Notice that the above set of equations is not adequate to determine the variables. When the equations for the balance of linear momentum at 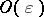 ,
, 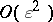 and
and 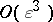 are appended to (a3), i.e.,
are appended to (a3), i.e.,
 | (a4) |
one obtains a determinate system of equations (a3)–(a4), referred to as the Oberbeck–Boussinesq equations. Thus, the Oberbeck–Boussinesq equations do not follow from retaining the perturbances of the same order in  . This perturbation procedure, discussed in [a3] in detail, also provides the corrections to the Oberbeck–Boussinesq equations at higher order of
. This perturbation procedure, discussed in [a3] in detail, also provides the corrections to the Oberbeck–Boussinesq equations at higher order of  .
.
A similar heuristic approach has been developed for the thermo-mechanical response of non-Newtonian fluids [a5].
Also, in the case of the thermo-mechanical response of solids, the constraint (a1) seems to be applicable. However, the counterparts to the Oberbeck–Boussinesq equations have not yet been established as there is no single model that enjoys the kind of widespread use as the Navier–Stokes equations. From the point of view of mathematical analysis, the Oberbeck–Boussinesq equations are an example of a coupled non-linear system that retain the salient features of the Navier–Stokes equations when temperature effects are included. See [a6] or [a7] for details.
References
| [a1] | A. Oberbeck, "Ueber die Wärmeleitung der Flüssigkeiten bei Berücksichtigung der Strömungen infolge von Temperaturdifferenzen" Ann. Phys. Chem. , VII (1879) pp. 271–292 |
| [a2] | J. Boussinesq, "Théorie analytique de la chaleur" , Gauthier-Villars (1903) |
| [a3] | K.R. Rajagopal, M. Ruzicka, A.R. Srinivasa, "On the Oberbeck–Boussinesq approximation" Math. Meth. Appl. Sci. , 6 (1996) pp. 1157–1167 |
| [a4] | S. Chandrasekar, "Hydrodynamic and hydromagnetic stability" , Oxford Univ. Press (1961) |
| [a5] | A.V. Shenoy, R.A. Mashelkar, "Thermal convenction in non-Newtonian fluids" J.P. Hartnett (ed.) T.F. Irvine (ed.) , Advances in Heat Transfer , 15 , Acad. Press (1982) pp. 143–225 |
| [a6] | C. Foias, O. Manley, R. Temam, "Attractors for the Bénard problem: existence and physical bounds on their fractal dimension" Nonlinear Anal. Theory Methods Appl. , 11 (1987) pp. 939–967 |
| [a7] | R. Temam, "Infinite-dimensional dynamical systems in mechanics and physics" , Springer (1997) (Edition: Second) |
Oberbeck-Boussinesq equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oberbeck-Boussinesq_equations&oldid=14912