O-minimal
Let 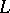 be a first-order language containing a binary relation symbol
be a first-order language containing a binary relation symbol  and let
and let 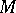 be an
be an 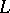 -structure (cf. Structure) in which
-structure (cf. Structure) in which 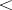 is interpreted as a total order (cf. Order (on a set)). Then
is interpreted as a total order (cf. Order (on a set)). Then  is called
is called  -minimal if every parametrically definable subset of
-minimal if every parametrically definable subset of 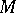 is a finite union of intervals of
is a finite union of intervals of 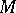 . An interval of
. An interval of 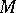 is a subset of the form
is a subset of the form  for some
for some 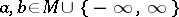 , where
, where 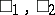 stand for
stand for 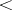 or
or 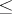 . For
. For 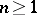 , a subset
, a subset 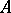 of the Cartesian product
of the Cartesian product 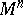 is called parametrically definable if there are an
is called parametrically definable if there are an 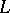 -formula
-formula 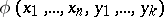 and
and 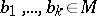 such that
such that
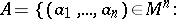 |
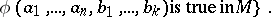 |
An elementary theory is called  -minimal if every model of it is
-minimal if every model of it is  -minimal.
-minimal.
This notion was introduced by L. van den Dries in [a2], while studying the expansion 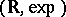 of the ordered field
of the ordered field 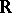 of the real numbers by the real exponential function (cf. Exponential function, real). He observed that the sets parametrically definable in Cartesian products
of the real numbers by the real exponential function (cf. Exponential function, real). He observed that the sets parametrically definable in Cartesian products 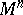 for an
for an  -minimal expansion
-minimal expansion  of
of 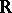 share many of the geometric properties of semi-algebraic sets (cf. Semi-algebraic set). For example, a semi-algebraic set has only finitely many connected components, each of them semi-algebraic (cf. [a1]), and van den Dries showed that this result remains true if one replaces "semi-algebraic" by "parametrically definable in an o-minimal expansion of R" . This is a finiteness theorem, and van den Dries aims to explain the other finiteness phenomena in real algebraic and real analytic geometry as consequences of
share many of the geometric properties of semi-algebraic sets (cf. Semi-algebraic set). For example, a semi-algebraic set has only finitely many connected components, each of them semi-algebraic (cf. [a1]), and van den Dries showed that this result remains true if one replaces "semi-algebraic" by "parametrically definable in an o-minimal expansion of R" . This is a finiteness theorem, and van den Dries aims to explain the other finiteness phenomena in real algebraic and real analytic geometry as consequences of  -minimality (cf. [a3]).
-minimality (cf. [a3]).
In [a6], J.F. Knight, A. Pillay and C. Steinhorn prove the following results.
1)  -minimality is preserved under elementary equivalence.
-minimality is preserved under elementary equivalence.
2) An ordered group is  -minimal if and only if it is divisible Abelian.
-minimal if and only if it is divisible Abelian.
3) An ordered ring is  -minimal if and only if it is a real closed field.
-minimal if and only if it is a real closed field.
4) Any parametrically definable unary function in an  -minimal structure is piecewise strictly monotone or constant, and continuous. The real closed field
-minimal structure is piecewise strictly monotone or constant, and continuous. The real closed field 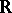 is
is  -minimal. The expansion of
-minimal. The expansion of 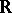 by restricted analytic functions (cf. Model theory of the real exponential function) is
by restricted analytic functions (cf. Model theory of the real exponential function) is  -minimal (cf. [a4]), as a consequence of Gabrielov's theorem of the complement that the complement of a subanalytic set is subanalytic (cf. [a5]). It follows from work of A. Wilkie [a7] that
-minimal (cf. [a4]), as a consequence of Gabrielov's theorem of the complement that the complement of a subanalytic set is subanalytic (cf. [a5]). It follows from work of A. Wilkie [a7] that 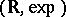 is
is  -minimal. His recent generalization of Gabrielov's theorem establishes the much stronger result that the expension of
-minimal. His recent generalization of Gabrielov's theorem establishes the much stronger result that the expension of 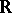 by Pfaffian chains of total functions is
by Pfaffian chains of total functions is  -minimal, see [a8]. A. Macintyre, van den Dries and D. Marker establish in [a4] the
-minimal, see [a8]. A. Macintyre, van den Dries and D. Marker establish in [a4] the  -minimality of
-minimality of 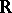 expanded by the restricted analytic functions and the exponential function. For a research account on
expanded by the restricted analytic functions and the exponential function. For a research account on  -minimal structures, see [a3].
-minimal structures, see [a3].
References
| [a1] | G.E. Collins, "Quantifier elimination for real closed fields by cylindrical algebraic decomposition, automata theory and formal language" , 2nd G.I. Conf. Kaiserslautern , Springer (1975) pp. 134–183 |
| [a2] | L. van den Dries, "Remarks on Tarski's problem concerning 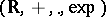 " G. Lolli (ed.) G. Longo (ed.) A. Marcja (ed.) , Logic Colloquium '82 , North-Holland (1984) pp. 97–121 " G. Lolli (ed.) G. Longo (ed.) A. Marcja (ed.) , Logic Colloquium '82 , North-Holland (1984) pp. 97–121 |
| [a3] | L. van den Dries, "o-minimal structures" W. Hodges (ed.) M. Hyland (ed.) C. Steinhorn (ed.) J. Truss (ed.) , Logic: From Foundations to Applications, European Logic Colloquium , Oxford (1996) pp. 137–185 |
| [a4] | L. van den Dries, A.J. Macintyre, D. Marker, "The elementary theory of restricted analytic fields with exponentiation" Ann. of Math. , 140 (1994) pp. 183–205 |
| [a5] | A. Gabrielov, "Projections of semi-analytic sets" Funct. Anal. Appl. , 2 (1968) pp. 282–291 |
| [a6] | J.F. Knight, A. Pillay, C. Steinhorn, "Definable sets in ordered structures I, II" Trans. Amer. Math. Soc. , 295 (1986) pp. 565–605 |
| [a7] | A.J. Wilkie, "Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function" J. Amer. Math. Soc. , 9 : 4 (1996) |
| [a8] | A.J. Wilkie, "A general theorem of the complement and new  -minimal expansions of the reals" , manuscript (1996) -minimal expansions of the reals" , manuscript (1996) |
O-minimal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=O-minimal&oldid=12517