Nyquist criterion
A necessary and sufficient condition for the stability of a linear closed-loop system formulated in terms of properties of the open-loop system.
Consider the linear single input-linear single output system with the following transfer function:
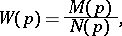 |
where it is assumed that the degree of the polynomial 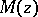 does not exceed that of the polynomial
does not exceed that of the polynomial 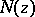 (i.e.
(i.e. 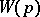 is a proper rational function). The original Nyquist criterion gives necessary and sufficient conditions for the stability of the closed-loop system with unity feedback
is a proper rational function). The original Nyquist criterion gives necessary and sufficient conditions for the stability of the closed-loop system with unity feedback 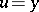 . This is done in terms of the complex-valued function
. This is done in terms of the complex-valued function 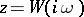 of the real variable
of the real variable 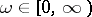 (the amplitude-phase characteristic of the open-loop system) which describes a curve in the complex
(the amplitude-phase characteristic of the open-loop system) which describes a curve in the complex  -plane, known as the Nyquist diagram. Suppose that the characteristic polynomial
-plane, known as the Nyquist diagram. Suppose that the characteristic polynomial 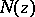 of the open-loop system has
of the open-loop system has  ,
, 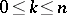 , roots with positive real part and
, roots with positive real part and 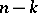 roots with negative real part. The Nyquist criterion is as follows: The closed-loop system is stable if and only if the Nyquist diagram encircles the point
roots with negative real part. The Nyquist criterion is as follows: The closed-loop system is stable if and only if the Nyquist diagram encircles the point 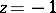 in the counter-clockwise sense
in the counter-clockwise sense 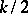 times. (An equivalent formulation is: The vector drawn from
times. (An equivalent formulation is: The vector drawn from 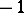 to the point
to the point 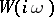 describes an angle
describes an angle 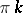 in the positive sense as
in the positive sense as 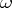 goes from
goes from  to
to 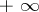 .)
.)
This criterion was first proposed by H. Nyquist [1] for feedback amplifiers; it is one of the frequency criteria for the stability of linear systems (similar, e.g., to the Mikhailov criterion, see [2], [3]). It is important to note that if the equations of some of the elements of the systems are unknown, the Nyquist diagram can be constructed experimentally, by feeding a harmonic signal of variable frequency to the input of the open feedback [4].
Generalizations of this criterion have since been developed for multivariable, infinite-dimensional and sampled-data systems, e.g. [5], , , .
References
| [1] | H. Nyquist, "Regeneration theory" Bell System Techn. J. , 11 : 1 (1932) pp. 126–147 |
| [2] | B.V. Bulgakov, "Oscillations" , Moscow (1954) (In Russian) |
| [3] | M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [4] | Ya.N. Roitenberg, "Automatic control" , Moscow (1978) (In Russian) |
| [5] | L.S. Gnoenskii, G.A. Kamenskii, L.E. El'sgol'ts, "Mathematical foundations of the theory of control systems" , Moscow (1969) (In Russian) |
Comments
For generalizations of the Nyquist criterion in various directions, see [a1].
References
| [a1] | C.A. Desoer, M. Vidyasagar, "Feedback systems: input-output properties" , Acad. Press (1975) |
| [a2] | C.A. Desoer, "A general formulation of the Nyquist stability criterion" IEEE Trans. Circuit Theory , CT-12 (1965) pp. 230–234 |
| [a3] | C.A. Desoer, Y.T. Wang, "On the generalized Nyquist stability criterion" IEEE Trans. Autom. Control , AC-25 (1980) pp. 187–196 |
| [a4] | F.M. Callier, C.A. Desoer, "On simplifying a graphical stability criterion for linear distributed feedback systems" IEEE Trans. Automat. Contr. , AC-21 (1976) pp. 128–129 |
| [a5] | J.M.E. Valenca, C.J. Harris, "Nyquist criterion for input-output stability of multivariable systems" Int. J. Control , 31 (1980) pp. 917–935 |
| [a6] | P. Faurre, M. Depeyrot, "Elements of system theory" , North-Holland (1977) |
Nyquist criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nyquist_criterion&oldid=13502