Number of divisors
From Encyclopedia of Mathematics
A function of a natural argument,  , equal to the number of natural divisors of the number
, equal to the number of natural divisors of the number  . This arithmetic function is denoted by
. This arithmetic function is denoted by  or
or  . The following formula holds:
. The following formula holds:
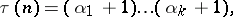 |
where
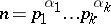 |
is the canonical expansion of  into prime factors. For prime numbers
into prime factors. For prime numbers  ,
,  , but there exists an infinite sequence of
, but there exists an infinite sequence of  for which
for which
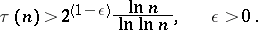 |
On the other hand, for all 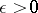 ,
,
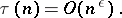 |
 is a multiplicative arithmetic function and is equal to the number of points with natural coordinates on the hyperbola
is a multiplicative arithmetic function and is equal to the number of points with natural coordinates on the hyperbola 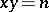 . The average value of
. The average value of  is given by Dirichlet's asymptotic formula (cf. Divisor problems). The function
is given by Dirichlet's asymptotic formula (cf. Divisor problems). The function 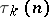 , which is the number of solutions of the equation
, which is the number of solutions of the equation 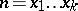 in natural numbers
in natural numbers  , is a generalization of the function
, is a generalization of the function 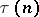 .
.
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
| [2] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XVI |
How to Cite This Entry:
Number of divisors. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Number_of_divisors&oldid=18293
Number of divisors. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Number_of_divisors&oldid=18293
This article was adapted from an original article by N.I. Klimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article