Nuclear space
A locally convex space for which all continuous linear mappings into an arbitrary Banach space are nuclear operators (cf. Nuclear operator). The concept of a nuclear space arose [1] in an investigation of the question: For what spaces are the analogues of Schwartz' kernel theorem valid (see Nuclear bilinear form)? The fundamental results in the theory of nuclear spaces are due to A. Grothendieck [1]. The function spaces used in analysis are, as a rule, Banach or nuclear spaces. Nuclear spaces play an important role in the spectral analysis of operators on Hilbert spaces (the construction of rigged Hilbert spaces, expansions in terms of generalized eigen vectors, etc.) (see [2]). Nuclear spaces are closely connected with measure theory on locally convex spaces (see [3]). Nuclear spaces can be characterized in terms of dimension-type invariants (approximative dimension, diametral dimension, etc.) (see [2], [4], [5]). One of these invariants is the functional dimension, which for many spaces consisting of entire analytic functions is the same as the number of variables on which these functions depend (see [2]).
In their properties, nuclear spaces are close to finite-dimensional spaces. Every bounded set in a nuclear space is pre-compact. If a nuclear space is complete (or at least quasi-complete, that is, every closed bounded set is complete), then it is semi-reflexive (that is, the space coincides with its second dual as a set of elements), and every closed bounded set in it is compact. If a quasi-complete nuclear space is a barrelled space, then it is also a Montel space (in particular, a reflexive space); any weakly-convergent countable sequence in this space converges also in the original topology. A normed space is nuclear if and only if it is finite dimensional. Every nuclear space has the approximation property: Any continuous linear operator in such a space can be approximated in the operator topology of pre-compact convergence by operators of finite rank (that is, continuous linear operators with finite-dimensional ranges). Nevertheless, there are nuclear Fréchet spaces (cf. Fréchet space) that do not have the bounded approximation property; in such a space the identity operator is not the limit of a countable sequence of operators of finite rank in the strong or weak operator topology [6]. Nuclear Fréchet spaces without a Schauder basis have been constructed, and they can have arbitrarily small diametral dimension, that is, they can be arbitrarily near (in a certain sense) to finite-dimensional spaces [7]. For nuclear spaces a counterexample to the problem of invariant subspaces has been constructed: In a certain nuclear Fréchet space one can find a continuous linear operator without non-trivial invariant closed subspaces [8].
Examples of nuclear spaces.
1) Let 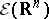 be the space of all (real or complex) infinitely-differentiable functions on
be the space of all (real or complex) infinitely-differentiable functions on 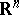 equipped with the topology of uniform convergence of all derivatives on compact subsets of
equipped with the topology of uniform convergence of all derivatives on compact subsets of 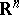 . The space
. The space 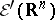 dual to
dual to 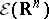 consists of all generalized functions (cf. Generalized function) with compact support. Let
consists of all generalized functions (cf. Generalized function) with compact support. Let 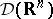 and
and 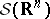 be the linear subspaces of
be the linear subspaces of 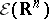 consisting, respectively, of functions with compact support and of functions that, together with all their derivatives, decrease faster than any power of
consisting, respectively, of functions with compact support and of functions that, together with all their derivatives, decrease faster than any power of 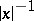 as
as 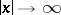 . The duals
. The duals 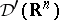 and
and 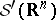 of
of 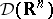 and
and 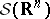 , relative to the standard topology, consist of all generalized functions and of all generalized functions of slow growth, respectively. The spaces
, relative to the standard topology, consist of all generalized functions and of all generalized functions of slow growth, respectively. The spaces 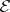 ,
,  ,
, 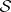 ,
, 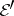 ,
, 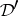 , and
, and 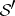 , equipped with the strong topology, are complete reflexive nuclear spaces.
, equipped with the strong topology, are complete reflexive nuclear spaces.
2) let  be an infinite matrix, where
be an infinite matrix, where 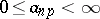 and
and 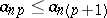 ,
,  . The space of sequences
. The space of sequences 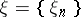 for which
for which 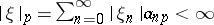 for all
for all 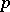 , with the topology defined by the semi-norms
, with the topology defined by the semi-norms 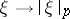 (cf. Semi-norm), is called a Köthe space, and is denoted by
(cf. Semi-norm), is called a Köthe space, and is denoted by  . This space is nuclear if and only if for any
. This space is nuclear if and only if for any 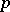 one can find a
one can find a 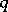 such that
such that 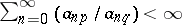 .
.
Heredity properties.
A locally convex space is nuclear if and only if its completion is nuclear. Every subspace (separable quotient space) of a nuclear space is nuclear. The direct sum, the inductive limit of a countable family of nuclear spaces, and also the product and the projective limit of any family of nuclear spaces, is again nuclear.
Let 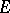 be an arbitrary locally convex space, and let
be an arbitrary locally convex space, and let 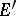 denote its dual equipped with the strong topology. If
denote its dual equipped with the strong topology. If 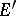 is nuclear, then
is nuclear, then 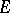 is called conuclear. If
is called conuclear. If 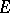 is arbitrary and
is arbitrary and 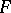 is a nuclear space, then the space
is a nuclear space, then the space 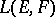 of continuous linear operators from
of continuous linear operators from 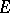 into
into 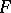 is nuclear with respect to the strong operator topology (simple convergence); if
is nuclear with respect to the strong operator topology (simple convergence); if 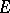 is semi-reflexive and conuclear, then
is semi-reflexive and conuclear, then  is nuclear also in the topology of bounded convergence.
is nuclear also in the topology of bounded convergence.
Metric and dually-metric nuclear spaces.
A locally convex space 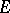 is called dually metric, or a space of type
is called dually metric, or a space of type 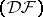 , if it has a countable fundamental system of bounded sets and if every (strongly) bounded countable union of equicontinuous subsets in
, if it has a countable fundamental system of bounded sets and if every (strongly) bounded countable union of equicontinuous subsets in 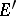 is equicontinuous (cf. Equicontinuity). Any strong dual of a metrizable locally convex space is dually metric; the converse is not true. If
is equicontinuous (cf. Equicontinuity). Any strong dual of a metrizable locally convex space is dually metric; the converse is not true. If 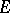 is a space of type
is a space of type 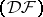 , then
, then 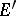 is of type
is of type 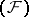 (a Fréchet space, that is, complete and metrizable). Examples of nuclear spaces of type
(a Fréchet space, that is, complete and metrizable). Examples of nuclear spaces of type 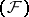 are Köthe spaces, and also
are Köthe spaces, and also 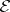 and
and 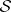 ; accordingly,
; accordingly, 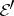 and
and 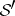 are nuclear spaces of type
are nuclear spaces of type 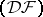 . The spaces
. The spaces 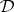 and
and 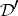 are neither metric nor dually metric.
are neither metric nor dually metric.
Metric and dually-metric nuclear spaces are separable, and if complete, they are reflexive. The transition  to the dual space establishes a one-to-one correspondence between nuclear spaces of type
to the dual space establishes a one-to-one correspondence between nuclear spaces of type 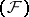 and complete nuclear spaces of type
and complete nuclear spaces of type 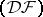 . If
. If 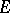 is a complete nuclear space of type
is a complete nuclear space of type 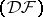 and if
and if 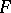 is a nuclear space of type
is a nuclear space of type 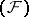 , then
, then 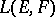 , equipped with the topology of bounded convergence, is nuclear and conuclear.
, equipped with the topology of bounded convergence, is nuclear and conuclear.
Every nuclear space of type 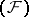 is isomorphic to a subspace of the space
is isomorphic to a subspace of the space 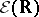 of infinitely-differentiable functions on the real line, that is,
of infinitely-differentiable functions on the real line, that is, 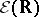 is a universal space for the nuclear spaces of type
is a universal space for the nuclear spaces of type 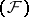 (see [10]). A Fréchet space
(see [10]). A Fréchet space 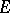 is nuclear if and only if every unconditionally-convergent series (cf. Unconditional convergence) in
is nuclear if and only if every unconditionally-convergent series (cf. Unconditional convergence) in 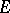 is absolutely convergent (that is, with respect to any continuous semi-norm). Spaces of holomorphic functions on nuclear spaces of types
is absolutely convergent (that is, with respect to any continuous semi-norm). Spaces of holomorphic functions on nuclear spaces of types 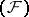 and
and 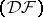 have been studied intensively (see [11]).
have been studied intensively (see [11]).
Tensor products of nuclear spaces, and spaces of vector functions.
The algebraic tensor product  of two locally convex spaces
of two locally convex spaces 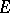 and
and 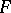 can be equipped with the projective and injective topologies, and then
can be equipped with the projective and injective topologies, and then  becomes a topological tensor product. The projective topology is the strongest locally convex topology in which the canonical bilinear mapping
becomes a topological tensor product. The projective topology is the strongest locally convex topology in which the canonical bilinear mapping 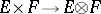 is continuous. The injective topology (or the topology of (bi) equicontinuous convergence) is induced by the natural imbedding
is continuous. The injective topology (or the topology of (bi) equicontinuous convergence) is induced by the natural imbedding 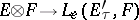 , where
, where 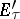 is the dual of
is the dual of 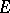 equipped with the Mackey topology
equipped with the Mackey topology 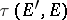 , and
, and 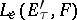 is the space of continuous linear mappings
is the space of continuous linear mappings  equipped with the topology of uniform convergence on equicontinuous sets in
equipped with the topology of uniform convergence on equicontinuous sets in 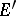 . Under this imbedding
. Under this imbedding 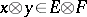 goes into the operator
goes into the operator 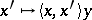 , where
, where 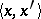 denotes the value of the functional
denotes the value of the functional 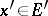 at
at 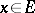 . The completion of
. The completion of  in the projective (respectively, injective) topology is denoted by
in the projective (respectively, injective) topology is denoted by 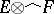 (respectively,
(respectively, 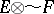 ).
).
For 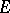 to be a nuclear space it is necessary and sufficient that for any locally convex space
to be a nuclear space it is necessary and sufficient that for any locally convex space 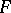 the projective and injective topologies in
the projective and injective topologies in  coincide, that is,
coincide, that is,
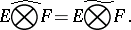 | (1) |
Actually, it suffices to require that (1) holds for  , the space of summable sequences, or for
, the space of summable sequences, or for 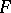 equal to a fixed space with an unconditional basis (see [12]). Nevertheless, there is a (non-nuclear) infinite-dimensional separable Banach space
equal to a fixed space with an unconditional basis (see [12]). Nevertheless, there is a (non-nuclear) infinite-dimensional separable Banach space 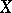 such that
such that  (see [13]). If
(see [13]). If 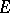 and
and 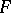 are complete spaces and
are complete spaces and 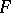 is nuclear, then the imbedding
is nuclear, then the imbedding 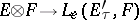 can be extended to an isomorphism between
can be extended to an isomorphism between 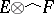 and
and 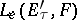 .
.
If 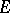 is a non-null nuclear space, then
is a non-null nuclear space, then  is nuclear if and only if
is nuclear if and only if 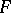 is nuclear. If
is nuclear. If 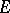 and
and 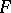 are both spaces of type
are both spaces of type 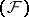 (or
(or 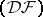 ) and if
) and if 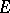 is nuclear, then
is nuclear, then 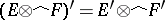 .
.
Let  be a complete nuclear space consisting of scalar functions (not all) on a certain set
be a complete nuclear space consisting of scalar functions (not all) on a certain set 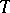 ; let also
; let also 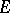 be the inductive limit (locally convex hull) of a countable sequence of spaces of type
be the inductive limit (locally convex hull) of a countable sequence of spaces of type 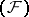 , and let the topology on
, and let the topology on 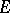 be not weaker than the topology of pointwise convergence of functions on
be not weaker than the topology of pointwise convergence of functions on 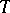 . Then for any complete space
. Then for any complete space 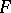 one can identify
one can identify 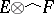 with the space of all mappings (vector functions)
with the space of all mappings (vector functions) 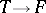 for which the scalar function
for which the scalar function 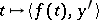 belongs to
belongs to 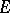 for all
for all 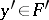 . In particular,
. In particular, 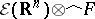 coincides with the space of all infinitely-differentiable vector functions on
coincides with the space of all infinitely-differentiable vector functions on 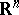 with values in
with values in 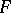 , and
, and 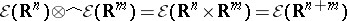 .
.
The structure of nuclear spaces.
Let 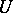 be a convex circled (i.e. convex balanced) neighbourhood of zero in a locally convex space
be a convex circled (i.e. convex balanced) neighbourhood of zero in a locally convex space 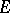 , and let
, and let 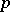 be the Minkowski functional (continuous semi-norm) corresponding to
be the Minkowski functional (continuous semi-norm) corresponding to 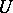 . Let
. Let 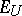 be the quotient space
be the quotient space 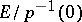 with the norm induced by
with the norm induced by 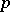 , and let
, and let 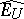 be the completion of the normed space
be the completion of the normed space 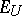 . There is defined a continuous canonical linear mapping
. There is defined a continuous canonical linear mapping 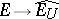 ; if
; if 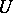 contains a neighbourhood
contains a neighbourhood 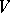 , then the continuous linear mapping
, then the continuous linear mapping 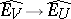 is defined canonically.
is defined canonically.
For a locally convex space 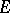 the following conditions are equivalent: 1)
the following conditions are equivalent: 1) 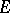 is nuclear; 2)
is nuclear; 2) 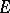 has a basis
has a basis 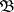 of convex circled neighbourhoods of zero such that for any
of convex circled neighbourhoods of zero such that for any 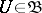 the canonical mapping
the canonical mapping 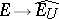 is a nuclear operator; 3) the mapping
is a nuclear operator; 3) the mapping 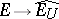 is nuclear for any convex circled neighbourhood
is nuclear for any convex circled neighbourhood  of zero in
of zero in 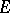 ; and 4) every convex circled neighbourhood
; and 4) every convex circled neighbourhood 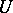 of zero in
of zero in 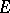 contains another such neighbourhood of zero,
contains another such neighbourhood of zero, 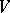 , such that the canonical mapping
, such that the canonical mapping 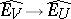 is nuclear.
is nuclear.
Let 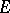 be a nuclear space. For any neighbourhood
be a nuclear space. For any neighbourhood 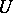 of zero in
of zero in 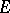 and for any
and for any 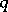 such that
such that 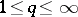 there is a convex circled neighbourhood
there is a convex circled neighbourhood 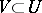 for which
for which 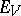 is (norm) isomorphic to a subspace of the space
is (norm) isomorphic to a subspace of the space 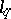 of sequences with summable
of sequences with summable 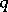 -th powers. Thus,
-th powers. Thus, 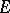 coincides with a subspace of the projective limit of a family of spaces isomorphic to
coincides with a subspace of the projective limit of a family of spaces isomorphic to 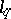 . In particular (the case
. In particular (the case  ), in any nuclear space
), in any nuclear space 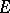 there is a basis of neighbourhoods of zero
there is a basis of neighbourhoods of zero 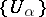 such that all the spaces
such that all the spaces 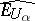 are Hilbert spaces; thus,
are Hilbert spaces; thus, 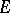 is Hilbertian, that is, the topology in
is Hilbertian, that is, the topology in 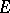 can be generated by a family of semi-norms each of which is obtained from a certain non-negative definite Hermitian form on
can be generated by a family of semi-norms each of which is obtained from a certain non-negative definite Hermitian form on 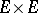 . Any complete nuclear space is isomorphic to the projective limit of a family of Hilbert spaces. A space
. Any complete nuclear space is isomorphic to the projective limit of a family of Hilbert spaces. A space 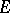 of type
of type 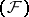 is nuclear if and only if it can be represented as the projective limit
is nuclear if and only if it can be represented as the projective limit 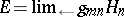 of a countable family of Hilbert spaces
of a countable family of Hilbert spaces 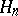 , such that the
, such that the 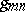 are nuclear operators (or, at least, Hilbert–Schmidt operators, cf. Hilbert–Schmidt operator) for
are nuclear operators (or, at least, Hilbert–Schmidt operators, cf. Hilbert–Schmidt operator) for 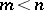 .
.
Bases in nuclear spaces.
In a nuclear space every equicontinuous basis is absolute. In a space of type 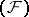 any countable basis (even if weak) is an equicontinuous Schauder basis (cf. Basis), so that in a nuclear space of type
any countable basis (even if weak) is an equicontinuous Schauder basis (cf. Basis), so that in a nuclear space of type 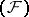 any basis is absolute (in particular, unconditional). A similar result holds for complete nuclear spaces of type
any basis is absolute (in particular, unconditional). A similar result holds for complete nuclear spaces of type 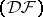 , and for all nuclear spaces for which the closed-graph theorem holds. A quotient space of a nuclear space of type
, and for all nuclear spaces for which the closed-graph theorem holds. A quotient space of a nuclear space of type 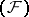 with a basis does not necessarily have a basis (see [4], [5], [6]).
with a basis does not necessarily have a basis (see [4], [5], [6]).
Let  be a nuclear space of type
be a nuclear space of type 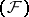 . A topology can be defined in
. A topology can be defined in 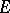 by a countable system of semi-norms
by a countable system of semi-norms 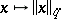 ,
, 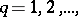 where
where 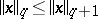 for all
for all 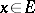 . If
. If 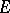 has a basis or a continuous norm, then the semi-norms
has a basis or a continuous norm, then the semi-norms  can be taken as norms. Let
can be taken as norms. Let 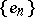 be a basis in
be a basis in 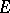 ; then any
; then any 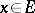 can be expressed as an (absolutely and unconditionally) convergent series
can be expressed as an (absolutely and unconditionally) convergent series
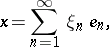 |
where the coordinates 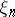 have the form
have the form 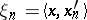 , and the functionals
, and the functionals 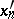 form a bi-orthogonal basis in
form a bi-orthogonal basis in 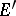 .
. 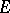 is isomorphic to the Köthe space
is isomorphic to the Köthe space 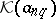 , where
, where 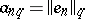 ; under this isomorphism
; under this isomorphism 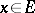 goes into the sequence
goes into the sequence 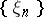 of its coordinates. A basis
of its coordinates. A basis  in
in  is equivalent to the basis
is equivalent to the basis 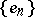 (that is, it can be obtained from
(that is, it can be obtained from 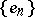 by an isomorphism) if and only if
by an isomorphism) if and only if 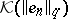 and
and 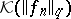 coincide as sets [4]. A basis
coincide as sets [4]. A basis 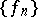 is called regular (or proper) if there is a system of norms
is called regular (or proper) if there is a system of norms 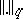 and a permutation
and a permutation 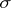 of indices such that
of indices such that 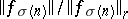 is monotone decreasing for all
is monotone decreasing for all 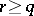 . If a nuclear space
. If a nuclear space 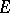 of type
of type 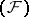 has a regular basis, then any two bases in
has a regular basis, then any two bases in 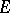 are quasi-equivalent (that is, they can be made equivalent by a permutation and a normalization of the elements of one of them). There are other sufficient conditions for all bases in
are quasi-equivalent (that is, they can be made equivalent by a permutation and a normalization of the elements of one of them). There are other sufficient conditions for all bases in 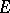 to be quasi-equivalent (see [4], [14]). A complete description of the class of nuclear spaces with this property is not known (1984).
to be quasi-equivalent (see [4], [14]). A complete description of the class of nuclear spaces with this property is not known (1984).
Example. The Hermite functions 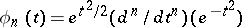 form a basis in the complete metric nuclear space
form a basis in the complete metric nuclear space  of smooth functions on the real line that are rapidly decreasing together with all their derivatives.
of smooth functions on the real line that are rapidly decreasing together with all their derivatives. 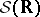 is isomorphic to
is isomorphic to 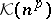 .
.
References
| [1] | A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires" , Amer. Math. Soc. (1955) |
| [2] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1968) (Translated from Russian) |
| [3] | R.A. Minlos, "Generalized random processes and their extension in measure" Trudy Moskov. Mat. Obshch. , 8 (1959) pp. 497–518 (In Russian) |
| [4] | B.S. Mityagin, "Approximate dimension and bases in nuclear spaces" Russian Math. Surveys , 16 : 4 pp. 59–127 Uspekhi Mat. Nauk , 16 : 4 (1961) pp. 63–132 |
| [5] | A. Pietsch, "Nuclear locally convex spaces" , Springer (1972) (Translated from German) |
| [6] | E. Dubinsky, "Structure of nuclear Fréchet spaces" , Springer (1979) |
| [7] | N.M. Zobin, B.S. Mityagin, "Examples of nuclear linear metric spaces without a basis" Funct. Anal. Appl. , 8 : 4 (1974) pp. 304–313 Funktsional. Anal. i Prilozhen. , 8 : 4 (1974) pp. 35–47 |
| [8] | A. Atzmon, "An operator without invariant subspaces on a nuclear Fréchet space" Ann. of Math. , 117 : 3 (1983) pp. 669–694 |
| [9] | H.H. Schaefer, "Topological vector spaces" , Springer (1971) |
| [10] | T. Komura, Y. Komura, "Ueber die Einbettung der nuklearen Räume in 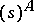 " Math. Ann. , 162 (1965–1966) pp. 284–288 " Math. Ann. , 162 (1965–1966) pp. 284–288 |
| [11] | S. Dineen, "Complex analysis in locally convex spaces" , North-Holland (1981) |
| [12] | K. John, V. Zizler, "On a tensor product characterization of nuclearity" Math. Ann. , 244 : 1 (1979) pp. 83–87 |
| [13] | G. Pisier, "Contre-example à une conjecture de Grothendieck" C.R. Acad. Sci. Paris , 293 (1981) pp. 681–683 (English abstract) |
| [14] | M.M. Dragilev, "Bases in Köthe spaces" , Rostov-on-Don (1983) (In Russian) |
Comments
A generalized function is also called a distribution, and a generalized function of slow growth is also called a tempered distribution.
Let 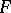 be a topological linear space,
be a topological linear space, 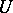 a neighbourhood of zero in
a neighbourhood of zero in 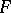 ,
, 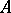 a set in
a set in 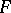 , and
, and  a (small) positive number. An
a (small) positive number. An  -set for
-set for 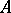 relative to a neighbourhood
relative to a neighbourhood 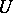 of zero is a set
of zero is a set 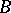 such that for every
such that for every 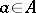 there is a
there is a 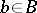 such that
such that 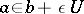 . Let
. Let 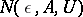 be the smallest number of elements in
be the smallest number of elements in  -sets for
-sets for 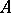 relative to
relative to 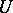 . The functional dimension of
. The functional dimension of 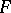 is defined by
is defined by
 |
where 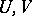 range over the neighbourhoods of zero in
range over the neighbourhoods of zero in 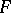 . Cf. [2], Sect. I.3.8 for more details.
. Cf. [2], Sect. I.3.8 for more details.
Let 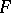 be a locally convex space and consider two neighbourhoods of zero
be a locally convex space and consider two neighbourhoods of zero 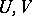 such that
such that 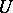 absorbs
absorbs 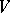 , i.e.
, i.e. 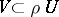 for some positive number
for some positive number 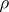 . Let
. Let
 |
 |
This number is called the  -th diameter of
-th diameter of 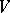 with respect to
with respect to 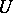 . The diametral dimension of a locally convex space is the collection of all sequences
. The diametral dimension of a locally convex space is the collection of all sequences 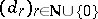 of non-negative numbers with the property that for each neighbourhood of zero
of non-negative numbers with the property that for each neighbourhood of zero 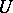 there is a neighbourhood
there is a neighbourhood 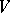 of zero absorbed by
of zero absorbed by 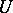 for which
for which  ,
, 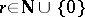 .
.
A locally convex space 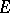 is nuclear if and only if for some (respectively, each) positive number
is nuclear if and only if for some (respectively, each) positive number  the sequence
the sequence 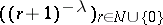 belongs to the diametral dimension of
belongs to the diametral dimension of 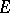 . See [5], Chapt. 9 for more details.
. See [5], Chapt. 9 for more details.
Let again 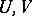 be neighbourhoods of zero of a locally convex space
be neighbourhoods of zero of a locally convex space  such that
such that 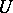 absorbs
absorbs 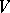 . The
. The  -content of
-content of 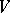 with respect to
with respect to 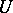 is the supremum
is the supremum  of all natural numbers
of all natural numbers 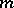 such that there are
such that there are 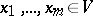 with
with 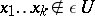 for all
for all 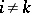 . The approximative dimension of a locally convex space
. The approximative dimension of a locally convex space  is the collection of all positive functions
is the collection of all positive functions 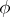 on
on 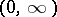 such that for each neighbourhood
such that for each neighbourhood 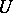 of zero there is a neighbourhood
of zero there is a neighbourhood 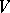 of zero absorbed by
of zero absorbed by 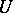 such that
such that
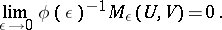 |
The number  is defined by the exponential rate of growth of
is defined by the exponential rate of growth of  as
as 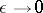 . More precisely,
. More precisely,
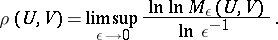 |
A locally convex space 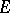 is nuclear if and only if for some (respectively, each) positive number
is nuclear if and only if for some (respectively, each) positive number  the following condition is satisfied: For each neighbourhood of zero
the following condition is satisfied: For each neighbourhood of zero 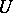 there is a neighbourhood
there is a neighbourhood 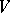 of zero absorbed by
of zero absorbed by 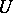 such that
such that 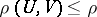 . Cf. [5], Chapt. 9 for more details.
. Cf. [5], Chapt. 9 for more details.
Let  be a bounded circled neighbourhood of a topological vector space
be a bounded circled neighbourhood of a topological vector space 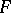 . The Minkowski functional associated to
. The Minkowski functional associated to 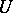 is defined by
is defined by
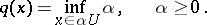 |
This is well-defined for each  since
since 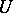 is absorbent (i.e. for each
is absorbent (i.e. for each 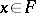 there is an
there is an 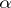 such that
such that 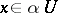 ). Cf. [a7], Sects. 15.10, 16.4.
). Cf. [a7], Sects. 15.10, 16.4.
References
| [a1] | A. Grothendieck, "Résumé de la théorie métrique des produits tensoriels topologiques" Bol. Soc. Mat. Sao-Paulo , 8 (1956) pp. 1–79 |
| [a2] | A. Grothendieck, "Topological vector spaces" , Gordon & Breach (1973) (Translated from French) |
| [a3] | H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German) |
| [a4] | G. Pisier, "Factorization of linear operators and geometry of Banach spaces" , Amer. Math. Soc. (1986) |
| [a5] | G. Pisier, "Counterexamples to a conjecture of Grothendieck" Acta. Math. , 151 (1983) pp. 181–208 |
| [a6] | J.F. Colombeau, "Differential calculus and holomorphy" , North-Holland (1982) |
| [a7] | G. Köthe, "Topological vector spaces" , 1 , Springer (1969) |
Nuclear space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nuclear_space&oldid=17938