Nuclear norm
trace norm
A norm on the space 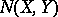 of nuclear operators (cf. Nuclear operator) mapping a Banach space
of nuclear operators (cf. Nuclear operator) mapping a Banach space 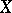 into a Banach space
into a Banach space 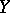 .
.
Let 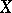 and
and 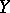 be Banach spaces over the field of real or complex numbers, let
be Banach spaces over the field of real or complex numbers, let 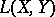 be the space of all continuous linear operators mapping
be the space of all continuous linear operators mapping 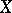 into
into 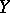 , and let
, and let 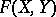 be the linear subspace consisting of operators of finite rank (that is, with finite-dimensional range). The Banach dual of
be the linear subspace consisting of operators of finite rank (that is, with finite-dimensional range). The Banach dual of 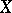 is denoted by
is denoted by 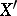 , and the value of a functional
, and the value of a functional 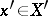 at a vector
at a vector 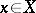 by
by 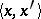 .
.
Every nuclear operator 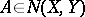 can be represented in the form
can be represented in the form
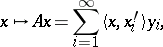 | (1) |
where 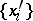 and
and 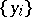 are sequences in
are sequences in 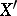 and
and 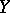 , respectively, such that
, respectively, such that
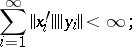 |
such representations are called nuclear. The quantity
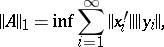 | (2) |
where the infimum is taken over all possible nuclear representations of the form (1), is called the nuclear norm of  . The space
. The space 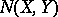 with this norm is a Banach space that contains
with this norm is a Banach space that contains 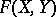 as a dense linear subspace. If
as a dense linear subspace. If 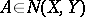 , then the adjoint operator
, then the adjoint operator 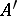 belongs to
belongs to 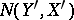 , and
, and 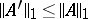 . Let
. Let  denote the usual operator norm in
denote the usual operator norm in 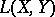 . Then
. Then 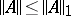 for all
for all 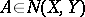 . If
. If 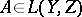 and
and 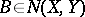 , then
, then 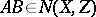 , and
, and 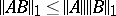 ; if
; if 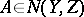 and
and 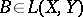 , then
, then 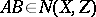 , and
, and 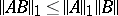 . Any operator
. Any operator 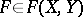 can be represented in the form
can be represented in the form
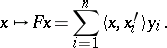 | (3) |
The quantity
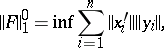 | (4) |
where the infimum is taken over all possible finite representations of the form (3), is called the finite nuclear norm of 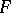 . The space
. The space 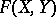 can be identified with the tensor product
can be identified with the tensor product 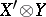 . Here, to an operator
. Here, to an operator 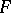 of the form (3) there corresponds the element
of the form (3) there corresponds the element
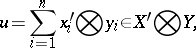 | (5) |
and the finite nuclear norm (4) goes into the norm
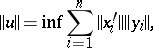 | (6) |
where the infimum is taken over all finite representations of  in the form (5). This norm is called the tensor (or cross) product of the norms in
in the form (5). This norm is called the tensor (or cross) product of the norms in 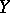 and in
and in 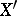 . The completion of
. The completion of  with respect to the norm (6) is denoted by
with respect to the norm (6) is denoted by 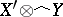 . The mapping
. The mapping 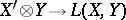 , under which the element (5) is mapped to the operator (3), can be extended to a continuous linear operator
, under which the element (5) is mapped to the operator (3), can be extended to a continuous linear operator 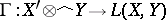 . The range of
. The range of 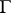 is
is 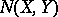 . If
. If 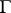 establishes a one-to-one correspondence between
establishes a one-to-one correspondence between 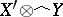 and
and 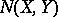 , then
, then 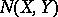 coincides with the closure of
coincides with the closure of 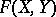 with respect to the norm (4); in this case the restriction of the nuclear norm to
with respect to the norm (4); in this case the restriction of the nuclear norm to 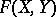 is the same as the finite nuclear norm. But, in general,
is the same as the finite nuclear norm. But, in general, 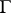 may have a non-trivial kernel, so that the nuclear norm is a quotient of the norm in
may have a non-trivial kernel, so that the nuclear norm is a quotient of the norm in 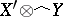 (see Nuclear operator).
(see Nuclear operator).
Let 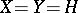 , where
, where 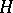 is a separable Hilbert space, let
is a separable Hilbert space, let 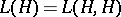 be the algebra of bounded operators on
be the algebra of bounded operators on 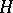 , and let
, and let 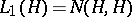 be the ideal of nuclear operators in
be the ideal of nuclear operators in 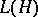 . In this case
. In this case 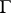 is one-to-one, for operators of finite rank the nuclear norm coincides with the finite nuclear norm, and each
is one-to-one, for operators of finite rank the nuclear norm coincides with the finite nuclear norm, and each 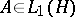 has a trace
has a trace 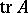 (see Nuclear operator). The nuclear norm of an operator
(see Nuclear operator). The nuclear norm of an operator 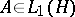 coincides with
coincides with 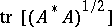 , where
, where 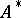 is the adjoint of
is the adjoint of 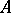 in
in  . The nuclear norm is connected with the Hilbert–Schmidt norm
. The nuclear norm is connected with the Hilbert–Schmidt norm 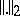 by
by 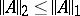 . The general form of a continuous linear functional on the Banach space
. The general form of a continuous linear functional on the Banach space 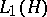 is given by
is given by
 | (7) |
where 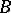 is an arbitrary operator from
is an arbitrary operator from 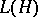 , and the norm of the functional (7) coincides with
, and the norm of the functional (7) coincides with 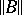 . Consequently,
. Consequently, 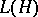 is isometric to the dual of
is isometric to the dual of 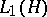 . Formula (7) also gives the general form of a linear functional on the closed subspace
. Formula (7) also gives the general form of a linear functional on the closed subspace 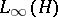 of
of 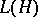 that consists of all completely-continuous (compact) operators; here
that consists of all completely-continuous (compact) operators; here 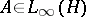 and
and 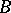 ranges over
ranges over 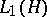 . In this case the norm of the functional (7) coincides with
. In this case the norm of the functional (7) coincides with 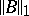 , that is, the space
, that is, the space 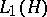 of nuclear operators with the nuclear norm is isometric to the dual of
of nuclear operators with the nuclear norm is isometric to the dual of 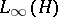 in the usual operator norm. These results have non-trivial generalizations to the case of operators on Banach spaces.
in the usual operator norm. These results have non-trivial generalizations to the case of operators on Banach spaces.
Example. Let 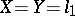 be the space of summable sequences. An operator
be the space of summable sequences. An operator  is contained in
is contained in 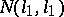 if and only if there is an infinite matrix
if and only if there is an infinite matrix 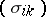 such that
such that 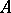 sends
sends 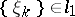 to
to 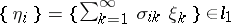 , and
, and 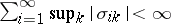 . In this case,
. In this case, 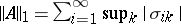 .
.
References
| [1] | A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires" , Amer. Math. Soc. (1955) |
| [2] | A. Pietsch, "Operator ideals" , North-Holland (1980) |
| [3] | A. Pietsch, "Nuclear locally convex spaces" , Springer (1972) (Translated from German) |
| [4] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , Transl. Math. Monogr. , 18 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [5] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1968) (Translated from Russian) |
| [6] | K. Maurin, "Methods of Hilbert spaces" , PWN (1967) |
| [7] | M.M. Day, "Normed linear spaces" , Springer (1958) |
Comments
References
| [a1] | A. Pietsch, "Eigenvalues and  -numbers" , Cambridge Univ. Press (1987) -numbers" , Cambridge Univ. Press (1987) |
| [a2] | A. Grothendieck, "Résumé de la théorie métrique des produits tensoriels topologiques" Bol. Soc. Mat. São Paulo , 8 (1956) pp. 1–79 |
| [a3] | H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German) |
Nuclear norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nuclear_norm&oldid=42221