Nuclear-C*-algebra
A 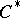 -algebra
-algebra 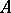 with the following property: For any
with the following property: For any 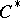 -algebra
-algebra 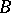 there is on the algebraic tensor product
there is on the algebraic tensor product 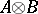 a unique norm such that the completion of
a unique norm such that the completion of 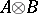 with respect to this norm is a
with respect to this norm is a 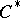 -algebra. Thus, relative to tensor products, nuclear
-algebra. Thus, relative to tensor products, nuclear 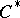 -algebras behave similarly to nuclear spaces (cf. Nuclear space) (although infinite-dimensional nuclear
-algebras behave similarly to nuclear spaces (cf. Nuclear space) (although infinite-dimensional nuclear 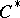 -algebras are not nuclear spaces). The class of nuclear
-algebras are not nuclear spaces). The class of nuclear  -algebras includes all type I
-algebras includes all type I 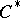 -algebras. This class is closed with respect to the inductive limit. If
-algebras. This class is closed with respect to the inductive limit. If 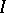 is a closed two-sided ideal in a
is a closed two-sided ideal in a 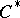 -algebra
-algebra 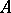 , then
, then  is nuclear if and only if
is nuclear if and only if 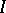 and
and  are. A subalgebra of a nuclear
are. A subalgebra of a nuclear 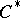 -algebra need not be a nuclear
-algebra need not be a nuclear 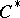 -algebra. The tensor product of two
-algebra. The tensor product of two 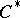 -algebras
-algebras 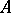 and
and 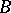 is nuclear if and only if
is nuclear if and only if 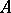 and
and 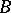 (both) are nuclear. If
(both) are nuclear. If 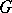 is an amenable locally compact group, then the enveloping
is an amenable locally compact group, then the enveloping 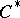 -algebra of the group algebra
-algebra of the group algebra 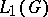 is nuclear (the converse is not true). Each factor representation of a nuclear
is nuclear (the converse is not true). Each factor representation of a nuclear 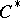 -algebra is hyperfinite, that is, the von Neumann algebra generated by this representation can be obtained from an increasing sequence of finite-dimensional factors (matrix algebras). Any factor state on a nuclear
-algebra is hyperfinite, that is, the von Neumann algebra generated by this representation can be obtained from an increasing sequence of finite-dimensional factors (matrix algebras). Any factor state on a nuclear 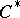 -subalgebra of a
-subalgebra of a 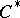 -algebra can be extended to a factor state on the whole algebra.
-algebra can be extended to a factor state on the whole algebra.
Let 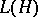 be the
be the 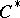 -algebra of all bounded linear operators on a Hilbert space
-algebra of all bounded linear operators on a Hilbert space 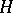 , and let
, and let 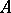 be a
be a 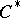 -algebra of operators on
-algebra of operators on 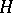 . If
. If 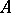 is nuclear, then its weak closure
is nuclear, then its weak closure 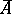 is an injective von Neumann algebra, that is, there is a projection
is an injective von Neumann algebra, that is, there is a projection 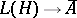 with norm one; in this case the commutant
with norm one; in this case the commutant 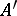 of
of  is also injective. An arbitrary
is also injective. An arbitrary 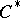 -algebra
-algebra 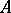 is nuclear if and only if its enveloping von Neumann algebra is injective.
is nuclear if and only if its enveloping von Neumann algebra is injective.
A 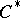 -algebra
-algebra 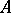 is nuclear if and only if it has the completely positive approximation property, i.e. the identity operator in
is nuclear if and only if it has the completely positive approximation property, i.e. the identity operator in 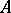 can be approximated in the strong operator topology by linear operators of finite rank with norm not exceeding 1, and with the additional property of "complete positivity" [1].
can be approximated in the strong operator topology by linear operators of finite rank with norm not exceeding 1, and with the additional property of "complete positivity" [1].
Every nuclear 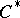 -algebra has the approximation and bounded approximation properties (see Nuclear operator). There is, however, a non-nuclear
-algebra has the approximation and bounded approximation properties (see Nuclear operator). There is, however, a non-nuclear  -algebra with the bounded approximation property. The
-algebra with the bounded approximation property. The  -algebra
-algebra 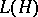 of all bounded operators on an infinite-dimensional Hilbert space
of all bounded operators on an infinite-dimensional Hilbert space 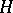 does not have the completely positive approximation property, or even the approximation property, so that
does not have the completely positive approximation property, or even the approximation property, so that 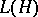 is not nuclear.
is not nuclear.
References
| [1] | E.C. Lance, "Tensor products and nuclear 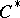 -algebras" R.V. Kadison (ed.) , Operator algebras and applications , Proc. Symp. Pure Math. , 38 , Amer. Math. Soc. (1982) pp. 379–399 -algebras" R.V. Kadison (ed.) , Operator algebras and applications , Proc. Symp. Pure Math. , 38 , Amer. Math. Soc. (1982) pp. 379–399 |
| [2] | O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , 1 , Springer (1979) |
Comments
References
| [a1] | R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , 1–2 , Acad. Press (1983) |
| [a2] | G.K. Pedersen, "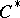 -algebras and their automorphism groups" , Acad. Press (1979) pp. Sect. 8.15.15 -algebras and their automorphism groups" , Acad. Press (1979) pp. Sect. 8.15.15 |
Nuclear-C*-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nuclear-C*-algebra&oldid=16622