Nowhere-dense set

of a topological space

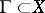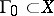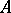A set defined by the following property: Every non-empty open set contains a non-empty open set such that . In other words, is nowhere dense if it is not dense in any non-empty open set.

Comments

Another characterization is: The interior of the closure of a nowhere-dense set is empty. If in a topological product infinitely many of the spaces 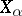are non-compact, then each compact subset of 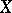is nowhere dense. A boundary set is the complement of a dense set, i.e. it satisfies 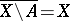. A set whose closure is a boundary set is nowhere dense. A non-empty complete metric space is of the second category, i.e. in it a countable union of nowhere-dense sets is nowhere dense (the Baire category theorem, cf. Baire theorem).

References

[a1]	A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)
[a2]	J.L. Kelley, "General topology" , v. Nostrand (1955) pp. 145