Normal subgroup

normal divisor, invariant subgroup

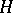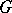A subgroup of a group for which the left decomposition of modulo 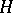is the same as the right one; in other words, a subgroup such that for any element 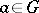the cosets 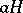and 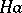are the same (as sets). In this case one also says that 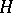is normal in 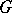and writes 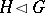; if also 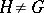, one writes 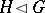. A subgroup 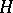is normal in 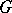if and only if it contains all 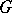-conjugates of any of its elements (see Conjugate elements), that is 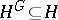. A normal subgroup can also be defined as one that coincides with all its conjugates, as a consequence of which it is also known as a self-conjugate subgroup.

For any homomorphism 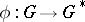the set 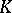of elements of 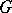that are mapped to the unit element of 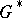(the kernel of the homomorphism 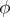) is a normal subgroup of 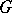, and conversely, every normal subgroup of 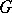is the kernel of some homomorphism; in particular, 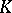is the kernel of the canonical homomorphism onto the quotient group .

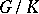The intersection of any set of normal subgroups is normal, and the subgroup generated by any system of normal subgroups of 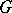is normal in .

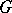Comments

A subgroup 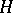of a group 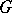is normal if 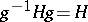for all 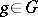, or, equivalently, if the normalizer 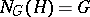, cf. Normalizer of a subset. A normal subgroup is also called an invariant subgroup because it is invariant under the inner automorphisms 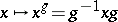, , 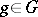of 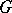. A subgroup that is invariant under all automorphisms is called a fully-invariant subgroup or characteristic subgroup. A subgroup that is invariant under all endomorphisms is a fully-characteristic subgroup.

References

[a1]	M. Hall jr., "The theory of groups" , Macmillan (1959) pp. 26
[a2]	C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. 5
[a3]	A.G. Kurosh, "The theory of groups" , 1 , Chelsea (1955) pp. Chapt. III (Translated from Russian)