Normal number
A real number 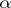 ,
, 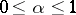 , having the following property: For every natural number
, having the following property: For every natural number  , any given
, any given  -tuple
-tuple 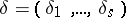 consisting of the symbols
consisting of the symbols 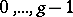 appears with asymptotic frequency
appears with asymptotic frequency 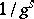 in the sequence
in the sequence
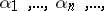 | (1) |
obtained from the expansion of 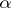 in an infinite fraction in base
in an infinite fraction in base 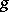 ,
,
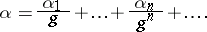 |
In more detail, let 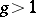 be a natural number and let
be a natural number and let
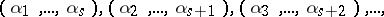 | (2) |
be the infinite sequence of  -tuples corresponding to (1). Let
-tuples corresponding to (1). Let 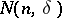 denote the number of occurrences of the tuple
denote the number of occurrences of the tuple 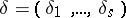 among the first
among the first  tuples of (2). The number
tuples of (2). The number
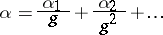 |
is said to be normal if for any number  and any given
and any given  -tuple
-tuple 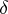 consisting of the symbols
consisting of the symbols 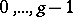 ,
,
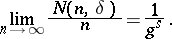 |
The concept of a normal number was introduced for 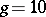 by E. Borel (see [1], [2], p. 197). He called a real number
by E. Borel (see [1], [2], p. 197). He called a real number 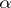 weakly normal to the base
weakly normal to the base 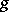 if
if
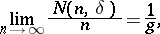 |
where 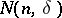 is the number of occurrences of
is the number of occurrences of 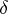 ,
, 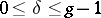 , among the first
, among the first  terms of the sequences
terms of the sequences 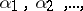 and normal if
and normal if  are weakly normal to the bases
are weakly normal to the bases 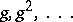 . He also showed that for a normal number
. He also showed that for a normal number
 |
for any  and any given
and any given  -tuple
-tuple  . Later it was proved (see [3], [4], and also [8]) that the last relation is equivalent to Borel's definition of a normal number.
. Later it was proved (see [3], [4], and also [8]) that the last relation is equivalent to Borel's definition of a normal number.
A number 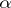 is called absolutely normal if it is normal with respect to every base
is called absolutely normal if it is normal with respect to every base 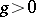 . The existence of normal and absolutely-normal numbers was established by Borel on the basis of measure theory. The construction of normal numbers in an explicit form was first achieved in [5]. Earlier (see [6], [7]) an effective procedure for constructing normal numbers was indicated. For other methods for constructing normal numbers and for connections between the concepts of normality and randomness see [8].
. The existence of normal and absolutely-normal numbers was established by Borel on the basis of measure theory. The construction of normal numbers in an explicit form was first achieved in [5]. Earlier (see [6], [7]) an effective procedure for constructing normal numbers was indicated. For other methods for constructing normal numbers and for connections between the concepts of normality and randomness see [8].
Uniform distribution of the fractional parts 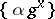 ,
, 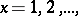 on the interval
on the interval 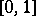 is equivalent to
is equivalent to  being normal.
being normal.
References
| [1] | E. Borel, "Les probabilités dénombrables et leurs applications arithmétiques" Rend. Circ. Math. Palermo , 27 (1909) pp. 247–271 |
| [2] | E. Borel, "Leçons sur la théorie des fonctions" , Gauthier-Villars (1928) |
| [3] | S. Pillai, "On normal numbers" Proc. Indian Acad. Sci. Sect. A , 12 (1940) pp. 179–184 |
| [4] | I. Niven, H. Zuckerman, "On the definition of normal numbers" Pacific J. Math. , 1 (1951) pp. 103–109 |
| [5] | D.G. Champernowne, "The construction of decimals normal in the scale of ten" J. London Math. Soc. , 8 (1933) pp. 254–260 |
| [6] | W. Sierpiński, "Démonstration élémentaire d'un théorème de M. Borel sur les nombres absolument normaux et détermination effective d'un tel nombre" Bull. Soc. Math. France , 45 (1917) pp. 127–132 |
| [7] | H. Lebesgue, "Sur certaines démonstrations d'existence" Bull. Soc. Math. France , 45 (1917) pp. 132–144 |
| [8] | A.G. Postnikov, "Arithmetic modelling of random processes" Trudy Mat. Inst. Steklov. , 57 (1960) (In Russian) |
Comments
Almost-all numbers are normal with respect to every base 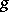 (see e.g. Theorem 8.11 in [a1]). It is not known whether familiar numbers like
(see e.g. Theorem 8.11 in [a1]). It is not known whether familiar numbers like 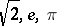 are normal or not. Normal numbers are potentially interesting in the context of random number generators. A normal number to a base
are normal or not. Normal numbers are potentially interesting in the context of random number generators. A normal number to a base 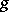 is necessarily irrational. The weakly-normal number (to base
is necessarily irrational. The weakly-normal number (to base 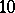 )
) 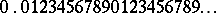 is of course rational. The number
is of course rational. The number 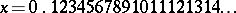 , obtained as
, obtained as 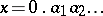 where
where 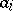 stands for the group of digits representing
stands for the group of digits representing 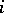 to base
to base 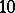 , is normal to base
, is normal to base 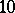 [5]. The same recipe works to obtain normal numbers to any given base.
[5]. The same recipe works to obtain normal numbers to any given base.
References
| [a1] | I. Niven, "Irrational numbers" , Math. Assoc. Amer. (1956) |
Normal number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_number&oldid=18704