Normal complex

of a semi-group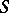

A non-empty subset 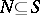satisfying the following condition: For any 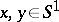(where 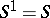when 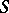contains a unit element and 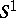is the semi-group obtained from 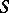by adjoining a unit element if 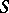does not have one) and any 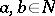it follows from 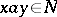that 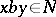. A subset 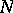is a normal complex of a semi-group 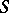if and only if 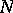is a class of some congruence on 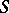(cf. Congruence (in algebra)).

References

[1]	E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian)