Normal basis theorem
Let  be a (finite-dimensional) Galois extension of a field
be a (finite-dimensional) Galois extension of a field  . Then there exists a normal basis for
. Then there exists a normal basis for  , that is, a basis consisting of an orbit of the Galois group
, that is, a basis consisting of an orbit of the Galois group  . Thus, an element
. Thus, an element  generates a normal basis if and only if its conjugates
generates a normal basis if and only if its conjugates  ,
,  , are linearly independent over
, are linearly independent over  ; see, e.g., [a3]. The element
; see, e.g., [a3]. The element  is called a normal basis generator or a free element in
is called a normal basis generator or a free element in 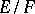 . A far-reaching strengthening of the normal basis theorem is due to D. Blessenohl and K. Johnsen [a1]: There exists an element
. A far-reaching strengthening of the normal basis theorem is due to D. Blessenohl and K. Johnsen [a1]: There exists an element 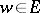 that is simultaneously free in
that is simultaneously free in 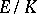 for every intermediate field
for every intermediate field  .
.
Such an element is called completely free (or completely normal). For the important special case where 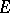 is a Galois field, a constructive treatment of normal bases and completely free elements can be found in [a2].
is a Galois field, a constructive treatment of normal bases and completely free elements can be found in [a2].
References
| [a1] | D. Blessenohl, K. Johnsen, "Eine Verschärfung des Satzes von der Normalbasis" J. Algebra , 103 (1986) pp. 141–159 |
| [a2] | D. Hachenberger, "Finite fields: Normal bases and completely free elements" , Kluwer Acad. Publ. (1997) |
| [a3] | N. Jacobson, "Basic algebra" , I , Freeman (1985) (Edition: Second) |
Normal basis theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_basis_theorem&oldid=11535