Difference between revisions of "Normal analytic space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 36: | Line 36: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.S. Abhyankar, "Local analytic geometry" , Acad. Press (1964) {{MR|0175897}} {{ZBL|0205.50401}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C. Houzel, "Géometrie analytique locale I" , ''Sem. H. Cartan Ann. 13 1960/61'' , '''2''' (1963) pp. Exp. 18–21 {{MR|}} {{ZBL|0121.15906}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Grauert, R. Remmert, "Komplexe Räume" ''Math. Ann.'' , '''136''' (1958) pp. 245–318 {{MR|0103285}} {{ZBL|0087.29003}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R. Narasimhan, "A note on Stein spaces and their normalisations" ''Ann. Scuola Norm. Sup. Pisa'' , '''16''' (1962) pp. 327–333 {{MR|0153870}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Y.T. Siu, G. Trautmann, "Gap sheaves and extensions of coherent analytic subsheaves" , Springer (1971) {{MR|0287033}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> H. Grauert, "Ueber Modifikationen und exzeptionelle analytische Mengen" ''Math. Ann.'' , '''146''' (1962) pp. 331–368 {{MR|}} {{ZBL|0178.42702}} {{ZBL|0173.33004}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> O. Zariski, P. Samuel, "Commutative algebra" , '''2''' , Springer (1960) {{MR|0120249}} {{ZBL|0121.27801}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> B.A. Fuks, "Theory of analytic functions of several complex variables" , '''1''' , Amer. Math. Soc. (1963) (Translated from Russian) {{MR|0174786}} {{MR|0168793}} {{ZBL|0138.30902}} </TD></TR></table> |
| Line 44: | Line 44: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Whitney, "Complex analytic varieties" , Addison-Wesley (1972) pp. Chapt. 8 {{MR|0387634}} {{ZBL|0265.32008}} </TD></TR></table> |
Revision as of 21:54, 30 March 2012
An analytic space the local rings of all points of which are normal, that is, are integrally-closed integral domains. A point  of an analytic space
of an analytic space  is said to be normal (one also says that
is said to be normal (one also says that  is normal at
is normal at  ) if the local ring
) if the local ring  is normal. In a neighbourhood of such a point the space has a reduced and irreducible model. Every simple (non-singular) point is normal. The simplest example of a normal analytic space is an analytic manifold.
is normal. In a neighbourhood of such a point the space has a reduced and irreducible model. Every simple (non-singular) point is normal. The simplest example of a normal analytic space is an analytic manifold.
In what follows the (complete non-discretely normed) ground field  is assumed to be algebraically closed. In this case the most complete results on normal analytic spaces have been obtained (see [1]) and a normalization theory has been constructed [2] that gives a natural link between arbitrary reduced analytic spaces and normal analytic spaces. Let
is assumed to be algebraically closed. In this case the most complete results on normal analytic spaces have been obtained (see [1]) and a normalization theory has been constructed [2] that gives a natural link between arbitrary reduced analytic spaces and normal analytic spaces. Let  be the set of points of an analytic space
be the set of points of an analytic space  that are not normal and let
that are not normal and let 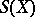 be the set of singular points of
be the set of singular points of 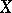 (cf. Singular point). Then:
(cf. Singular point). Then:
1) 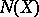 and
and 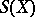 are closed analytic subspaces of
are closed analytic subspaces of 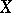 , and
, and 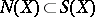 ;
;
2) for 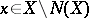 ,
,
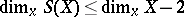 |
(that is, a normal analytic space is smooth in codimension 1);
3) if 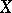 is a complete intersection at
is a complete intersection at  and if the above inequality holds, then
and if the above inequality holds, then 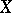 is normal at that point.
is normal at that point.
A normalization of a reduced analytic space 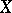 is a pair
is a pair 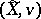 , where
, where 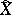 is a normal analytic space and
is a normal analytic space and 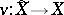 is a finite surjective analytic mapping inducing an isomorphism of the open sets
is a finite surjective analytic mapping inducing an isomorphism of the open sets
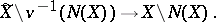 |
The normalization is uniquely determined up to an isomorphism, that is, if 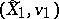 and
and 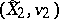 are two normalizations,
are two normalizations,
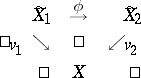 |
then there exists a unique analytic isomorphism  such that the diagram commutes. The normalization exists and has the following properties. For every point
such that the diagram commutes. The normalization exists and has the following properties. For every point 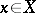 the set of irreducible components of
the set of irreducible components of 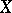 at
at  is in one-to-one correspondence with
is in one-to-one correspondence with 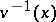 . The fibre at
. The fibre at 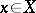 of the direct image
of the direct image 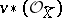 of the structure sheaf
of the structure sheaf 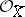 is naturally isomorphic to the integral closure of the ring
is naturally isomorphic to the integral closure of the ring 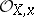 in its complete ring of fractions.
in its complete ring of fractions.
The concept of a normal analytic space over 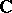 can be introduced in terms of analytic continuation of holomorphic functions [3]. Namely, a reduced complex space is normal if and only if Riemann's first theorem on the removal of singularities holds for it: If
can be introduced in terms of analytic continuation of holomorphic functions [3]. Namely, a reduced complex space is normal if and only if Riemann's first theorem on the removal of singularities holds for it: If 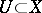 is an open subset and
is an open subset and 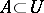 is a closed analytic subset not containing irreducible components of
is a closed analytic subset not containing irreducible components of 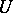 , then any function that is holomorphic on
, then any function that is holomorphic on 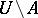 and locally bounded on
and locally bounded on 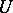 has a unique analytic continuation to a holomorphic function on
has a unique analytic continuation to a holomorphic function on 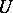 . For normal complex spaces Riemann's second theorem on the removal of singularities also holds: If
. For normal complex spaces Riemann's second theorem on the removal of singularities also holds: If 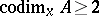 at every point
at every point 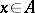 , then the analytic continuation in question is possible without the requirement that the function is bounded. A reduced complex space
, then the analytic continuation in question is possible without the requirement that the function is bounded. A reduced complex space 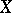 is normal if and only if for every open set
is normal if and only if for every open set 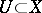 the restriction mapping of holomorphic functions
the restriction mapping of holomorphic functions
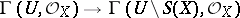 |
is bijective. The property of being normal can also be phrased in the language of local cohomology — it is equivalent to 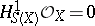 (see [5]). For any reduced complex space
(see [5]). For any reduced complex space 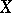 one can define the sheaf
one can define the sheaf 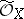 of rings of germs of weakly holomorphic functions, that is, functions satisfying the conditions of Riemann's first theorem. It turns out that the ring
of rings of germs of weakly holomorphic functions, that is, functions satisfying the conditions of Riemann's first theorem. It turns out that the ring 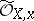 is finite as an
is finite as an 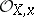 -module and equal to the integral closure of
-module and equal to the integral closure of 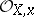 in its complete ring of fractions. In other words,
in its complete ring of fractions. In other words, 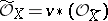 , where
, where 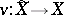 is the normalization mapping.
is the normalization mapping.
A normal complex space can also be characterized in the following manner: A complex space is normal if and only if every point of it has a neighbourhood that admits an analytic covering onto a domain of 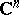 (see [3], [8]).
(see [3], [8]).
A reduced complex space 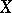 is a Stein space if and only if its normalization
is a Stein space if and only if its normalization  has this property (see [4]). To normal complex spaces one can extend the concept of a Hodge metric (see Kähler metric). Kodaira's projective imbedding theorem [6] carries over to compact normal spaces with such a metric.
has this property (see [4]). To normal complex spaces one can extend the concept of a Hodge metric (see Kähler metric). Kodaira's projective imbedding theorem [6] carries over to compact normal spaces with such a metric.
In algebraic geometry one examines analogues of normal analytic spaces: normal algebraic varieties (see Normal scheme). For algebraic varieties over a complete non-discretely normed field the two concepts are the same (see [7], [1]).
References
| [1] | S.S. Abhyankar, "Local analytic geometry" , Acad. Press (1964) MR0175897 Zbl 0205.50401 |
| [2] | C. Houzel, "Géometrie analytique locale I" , Sem. H. Cartan Ann. 13 1960/61 , 2 (1963) pp. Exp. 18–21 Zbl 0121.15906 |
| [3] | H. Grauert, R. Remmert, "Komplexe Räume" Math. Ann. , 136 (1958) pp. 245–318 MR0103285 Zbl 0087.29003 |
| [4] | R. Narasimhan, "A note on Stein spaces and their normalisations" Ann. Scuola Norm. Sup. Pisa , 16 (1962) pp. 327–333 MR0153870 |
| [5] | Y.T. Siu, G. Trautmann, "Gap sheaves and extensions of coherent analytic subsheaves" , Springer (1971) MR0287033 |
| [6] | H. Grauert, "Ueber Modifikationen und exzeptionelle analytische Mengen" Math. Ann. , 146 (1962) pp. 331–368 Zbl 0178.42702 Zbl 0173.33004 |
| [7] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , Springer (1960) MR0120249 Zbl 0121.27801 |
| [8] | B.A. Fuks, "Theory of analytic functions of several complex variables" , 1 , Amer. Math. Soc. (1963) (Translated from Russian) MR0174786 MR0168793 Zbl 0138.30902 |
Comments
References
| [a1] | H. Whitney, "Complex analytic varieties" , Addison-Wesley (1972) pp. Chapt. 8 MR0387634 Zbl 0265.32008 |
Normal analytic space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_analytic_space&oldid=18341