Non-self-adjoint operator
A linear operator in a Hilbert space the spectral analysis of which cannot be made to fit into the framework of the theory of self-adjoint operators (cf. Self-adjoint operator) and its simplest generalizations: the theory of unitary operators (cf. Unitary operator) and the theory of normal operators (cf. Normal operator). Non-self-adjoint operators arise in the discussion of processes that proceed without conservation of energy: in problems with friction, in the theory of open resonators, in problems of inelastic scattering, and others. Certain self-adjoint problems, in which by separation of variables an operator-valued function 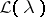 appears that depends non-linearly on a spectral parameter
appears that depends non-linearly on a spectral parameter 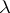 , also lead to a study of non-self-adjoint operators. Many of the propositions referring to the theory of non-self-adjoint operators are valid also for operators acting in arbitrary Banach spaces,
, also lead to a study of non-self-adjoint operators. Many of the propositions referring to the theory of non-self-adjoint operators are valid also for operators acting in arbitrary Banach spaces, 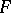 -spaces, topological vector spaces, etc.
-spaces, topological vector spaces, etc.
The most extensive method in the study of non-self-adjoint operators is that of evaluating the resolvent, which makes use of the theory of analytic functions, of asymptotic expansions, etc.
The first works concerned with the theory of non-self-adjoint operators were by G. Birkhoff, Ya.D. Tamarkin, V.A. Steklov, and others, in the investigation of problems for ordinary differential equations. These studies applied Cauchy's method of contour integration to the resolvent.
For non-self-adjoint partial differential operators effective methods of research were lacking for a long time. This can be explained by the complicated structure of the resolvent of such an operator as an analytic function.
In the development of a general theory of non-self-adjoint operators (in particular, partial differential operators) an important role was played by the work of M.V. Keldysh [1] (see also [2]). He studied an equation of the form
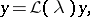 | (1) |
where 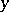 is an element of a certain Hilbert space
is an element of a certain Hilbert space 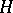 and the operator
and the operator 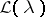 has the representation
has the representation
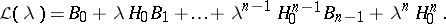 |
Here 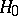 is a completely-continuous invertible self-adjoint operator of finite order and the
is a completely-continuous invertible self-adjoint operator of finite order and the 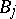 ,
, 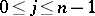 , are arbitrary completely-continuous operators. (A completely-continuous operator
, are arbitrary completely-continuous operators. (A completely-continuous operator 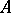 acting on a Hilbert space is said to be an operator of finite order if
acting on a Hilbert space is said to be an operator of finite order if 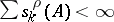 for some
for some 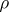 ,
, 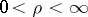 ; the
; the 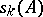 denote the singular numbers of
denote the singular numbers of 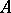 , that is, the eigen values of
, that is, the eigen values of  .) The eigen values of (1) are those
.) The eigen values of (1) are those 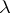 for which the equation has non-trivial solutions
for which the equation has non-trivial solutions 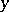 ; these solutions are called eigen vectors.
; these solutions are called eigen vectors.
Under the assumptions made above the spectrum of (1) is discrete. Since 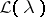 is non-self-adjoint, apart from the eigen vectors there naturally arise (in the presence of a multiple spectrum) associated vectors. In [1] a chain is constructed of associated vectors
is non-self-adjoint, apart from the eigen vectors there naturally arise (in the presence of a multiple spectrum) associated vectors. In [1] a chain is constructed of associated vectors 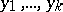 corresponding to an eigen value
corresponding to an eigen value 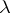 and eigen vector
and eigen vector 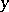 according to the rule
according to the rule
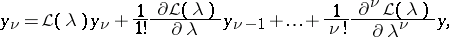 | (2) |
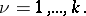 |
The system of eigen vectors and associated vectors of 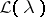 is said to be
is said to be  -fold complete if any
-fold complete if any  vectors
vectors 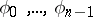 of
of 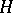 can be approximated in the norm of
can be approximated in the norm of 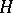 with arbitrary accuracy by finite linear combinations of the form
with arbitrary accuracy by finite linear combinations of the form
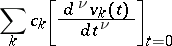 |
with the same coefficients 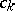 . Here
. Here 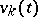 a is vector-valued function of the form
a is vector-valued function of the form
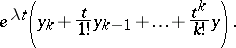 |
The definition of  -fold completeness is, naturally, connected with the solution of the Cauchy problem for the non-stationary equation corresponding to (1).
-fold completeness is, naturally, connected with the solution of the Cauchy problem for the non-stationary equation corresponding to (1).
According to a theorem of Keldysh, under the assumptions made on the coefficients of 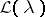 the system of all eigen vectors and associated vectors of
the system of all eigen vectors and associated vectors of 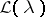 is
is  -fold complete in
-fold complete in 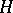 . In [1] he also proved that the eigen values of
. In [1] he also proved that the eigen values of  can be approximated asymptotically on rays with
can be approximated asymptotically on rays with 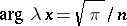 . In the proof of completeness Keldysh developed a new method for evaluating the resolvent of an abstract completely-continuous non-self-adjoint operator of finite order. Here emerged the special role played in the completeness problem by Volterra operators, i.e. completely-continuous operators with a single point of the spectrum at zero. In establishing the asymptotic behaviour of the eigen values, Keldysh [3] used a new Tauberian theorem due to him.
. In the proof of completeness Keldysh developed a new method for evaluating the resolvent of an abstract completely-continuous non-self-adjoint operator of finite order. Here emerged the special role played in the completeness problem by Volterra operators, i.e. completely-continuous operators with a single point of the spectrum at zero. In establishing the asymptotic behaviour of the eigen values, Keldysh [3] used a new Tauberian theorem due to him.
Keldysh's research was continued by many authors. His theorem was extended in [4] to the case when the operator 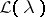 depends rationally on
depends rationally on 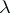 .
.
In [5]–[7] the equation 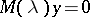 with
with 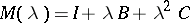 is considered, where
is considered, where 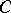 is a completely-continuous positive-definite operator and
is a completely-continuous positive-definite operator and 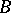 is a bounded self-adjoint operator. A generalization of Pontryagin's theorem (see [8]) on the existence of a maximal
is a bounded self-adjoint operator. A generalization of Pontryagin's theorem (see [8]) on the existence of a maximal 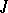 -non-negative invariant subspace for a
-non-negative invariant subspace for a 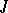 -self-adjoint operator
-self-adjoint operator 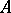 made it possible (see [6] and [7]) to establish the two-fold completeness of all eigen vectors and associated vectors of
made it possible (see [6] and [7]) to establish the two-fold completeness of all eigen vectors and associated vectors of 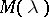 in situations important for applications, and also the one-fold completeness of the subsystem corresponding to the spectrum situated in the left (or right) half-plane. These results have been developed much further.
in situations important for applications, and also the one-fold completeness of the subsystem corresponding to the spectrum situated in the left (or right) half-plane. These results have been developed much further.
The summability of Fourier series in eigen vectors and associated vectors of a completely-continuous operator 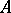 of finite order
of finite order 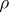 has been established (see [9]) if the eigen values of the quadratic form
has been established (see [9]) if the eigen values of the quadratic form 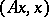 lie in a sector of the complex plane with opening angle less than
lie in a sector of the complex plane with opening angle less than 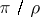 . (For applications of this theorem and further generalizations of it see [10] and the references there.)
. (For applications of this theorem and further generalizations of it see [10] and the references there.)
The question when the system of eigen vectors and associated vectors forms a basis in the Hilbert space has been studied in a number of papers. Most general conditions under which the system of eigen vectors and associated vectors of a dissipative completely-continuous operator forms a basis are found in [12].
In the case of singular differential operators with discrete spectrum a number of subtle results have been obtained (see [11] and [13]) on the completeness of the eigen functions and associated functions of a Sturm–Liouville operator with complex potential. Important results have been obtained for the case of an elliptic operator (see [14]). Keldysh's theorem has been generalized to the case of generalized eigen functions and associated functions of non-self-adjoint elliptic operators (see [15], [16]).
An attempt to carry over the theorem on the reduction to Jordan form of a finite-dimensional operator to the infinite-dimensional case has led to the construction of a triangular integral representation. For completely-continuous operators 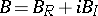 , where
, where 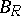 and
and 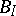 are self-adjoint and
are self-adjoint and 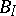 is of finite order, an analogue has been obtained of Schur's theorem on the unitary equivalence of
is of finite order, an analogue has been obtained of Schur's theorem on the unitary equivalence of 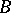 to a triangular operator (see [17]). A special place in the problem of triangular representation is occupied by Volterra operators.
to a triangular operator (see [17]). A special place in the problem of triangular representation is occupied by Volterra operators.
A special role in this problem is played by von Neumann's theorem, stating that a completely-continuous linear operator in a Hilbert space has a non-trivial invariant subspace; an arbitrary bounded linear operator in a Banach space need not have an invariant subspace; the corresponding problem for the case of a Hilbert space is still open (1989). A Volterra operator is said to be a unicellular operator if for any two invariant subspaces 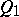 and
and 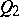 of it either
of it either 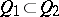 or
or 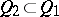 . In [18] a necessary and sufficient condition was found for an operator
. In [18] a necessary and sufficient condition was found for an operator  to be a unicellular operator under the assumption that
to be a unicellular operator under the assumption that 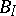 is nuclear and non-negative definite; this condition can be stated in terms of the growth of the resolvent of
is nuclear and non-negative definite; this condition can be stated in terms of the growth of the resolvent of 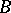 as
as 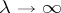 . A simple sufficient condition for being a unicellular operator is indicated in [19].
. A simple sufficient condition for being a unicellular operator is indicated in [19].
Non-self-adjoint operators with a continuous spectrum were first studied by M.A. Naimark (see [20], [21]), who obtained an expansion in a Fourier integral, connected with the non-self-adjoint problem
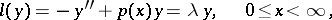 | (3) |
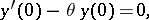 | (4) |
where 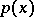 is a complex-valued function subject to the condition
is a complex-valued function subject to the condition
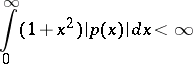 | (5) |
and 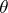 is a complex number. The results in [20] imply, in particular, that in a neighbourhood of points of the real axis where
is a complex number. The results in [20] imply, in particular, that in a neighbourhood of points of the real axis where 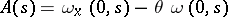 vanishes
vanishes 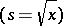 , the spectral projections of the operator (3)–(4) are unbounded. (Here
, the spectral projections of the operator (3)–(4) are unbounded. (Here 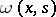 denotes the solution of (3) for which
denotes the solution of (3) for which 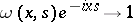 as
as 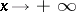 , the Jost solution.) In [20], the real zeros of
, the Jost solution.) In [20], the real zeros of 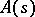 are called spectral singularities. In [22] a generalization of the results of [20] to the case of the Schrödinger equation in the three-dimensional space is obtained. In a further development of [20] it has been proved (see [23]) that in general (without a restriction of type (5)) the spectral function of a differential operator must be regarded as a continuous linear functional on a certain topological space.
are called spectral singularities. In [22] a generalization of the results of [20] to the case of the Schrödinger equation in the three-dimensional space is obtained. In a further development of [20] it has been proved (see [23]) that in general (without a restriction of type (5)) the spectral function of a differential operator must be regarded as a continuous linear functional on a certain topological space.
In [24] a system of non-self-adjoint equations is studied with singular points whose position depends on the spectral parameter. These systems occur in the theory of shells without moments (cf. Shell theory). For such systems asymptotic properties of the solutions have been established, and also solvability theorems of Cauchy type have been proved. Completeness theorems for the system of eigen functions and associated functions of non-self-adjoint integro-differential operators generating a non-regular problem have been established.
An important problem in the theory of non-self-adjoint operators is the expansion of the kernel of the Green operator of a biorthogonal series in eigen functions and associated functions and also the question of a basis. Tamarkin [25] has studied the expansion of a summable function in a series of eigen functions and associated functions of a regular problem, and also the question of equiconvergence with a trigonometric Fourier series. Later it was proved (see , [27]) that for non-regular problems equiconvergence with a trigonometric series does not hold.
For strongly-regular conditions the system of eigen functions and associated functions forms a basis in 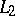 . It has been proved (see [28], [29]) that this system not only forms a basis, but even a so-called Riesz basis.
. It has been proved (see [28], [29]) that this system not only forms a basis, but even a so-called Riesz basis.
In [30] an important method has been developed for studying the basis property and the uniform convergence of the expansions in eigen functions and associated functions of an ordinary non-self-adjoint operator. This method is a further development of the ideas applied in the investigation of self-adjoint problems. A new treatment for the eigen functions and associated functions has been proposed, making it possible to dispense with the specific form of the boundary conditions; general ordinary differential operators or pencils of such operators are considered and necessary and sufficient conditions have been established for the basis property of the eigen functions and associated functions of such operators, as well as a criterion for equiconvergence. The method is based only on a mean value formula for the eigen functions and associated functions (see also [31]). It also turns out that if the operator has infinitely many associated functions, then the basis property depends on the choice of the latter (see [32]).
For non-self-adjoint elliptic operators there is convergence (see [33]) of a certain sequence of means of Poisson type of the partial sums of the biorthogonal series, that is, a summation method has been proposed.
Expansions in eigen functions and associated functions of non-regular problems were first obtained for problems of the form  ,
, 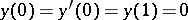 . It has been proved (see ) that expansions in uniformly convergent series of this form can hold for functions satisfying a certain analyticity condition.
. It has been proved (see ) that expansions in uniformly convergent series of this form can hold for functions satisfying a certain analyticity condition.
Among the fundamental studies is the problem (see [34]) in which the perturbation of the spectrum of the Laplace operator under a change of domain is studied. Here for the first time the role of the capacity of the set which is varying on the spectrum of the operator became manifest. These methods were successfully applied in the study of non-self-adjoint operators.
Regularization methods, the basics of which were expounded in [35], are successfully used in the theory of non-self-adjoint operators. An example is the problem of regularized traces (cf. Trace) of non-self-adjoint operators. The first paper on the theory of traces was [36], where the regularized trace of a Sturm–Liouville operator was computed. More general results in the theory of operator traces were obtained in [37] and [38]. It turns out that trace formulas for ordinary non-self-adjoint differential operators depending in a complicated manner on the spectral parameter can be obtained as consequences of the formulas for regularized sums of roots of a certain class of entire functions. (The traces of singular operators and partial differential operators are considered in [38], [39].)
Among the important works in which new methods and ideas in the theory of non-self-adjoint operators were developed one counts also the survey lecture [40].
The construction of a definitive theory of non-self-adjoint operators is far from complete (1989). On the one hand, in the theory itself there are new trends of research, such as scattering theory [41], the construction of the theory of contraction operators [42], the method of the canonical Maslov operator [43], the theory of spectral operators [44], and others; on the other hand, research on applied problems, mechanics and mathematical physics suggests new ways of developing this theory.
References
| [1] | M.V. Keldysh, "On eigenvalues and eigenfunctions of some classes of nonselfadjoint equations" Dokl. Akad. Nauk SSSR , 77 : 1 (1951) pp. 11–14 (In Russian) |
| [2] | M.V. Keldysh, "On the completeness of the eigenfunctions of some class of non-selfadjoint linear operators" Russian Math. Surveys , 26 : 4 (1971) pp. 15–44 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 15–41 |
| [3] | M.V. Keldysh, "On a Tauberian theorem" Trudy Mat. Inst. Steklov. , 38 (1951) pp. 77–86 (In Russian) |
| [4] | D.E. Allakhverdiev, "On completeness of a system of eigenelements and associated elements of a nonselfadjoint operator close to normal" Dokl. Akad. Nauk SSSR , 115 : 2 (1957) pp. 207–210 (In Russian) |
| [5] | H.K. Langer, "On 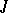 -Hermitian operators" Soviet Math. Dokl. , 1 : 4 (1960) pp. 1052–1055 Dokl. Akad. Nauk SSSR , 134 : 2 (1960) pp. 263–266 -Hermitian operators" Soviet Math. Dokl. , 1 : 4 (1960) pp. 1052–1055 Dokl. Akad. Nauk SSSR , 134 : 2 (1960) pp. 263–266 |
| [6] | M.G. Krein, "A new application of the fixed-point principle in the theory of operators on a space with indefinite metric" Soviet Math. Dokl. , 5 : 1 (1964) pp. 266–269 Dokl. Akad. Nauk SSSR , 154 : 5 (1964) pp. 1023–1026 |
| [7] | H.K. Langer, M.G. Krein, "Applications of function theory in the mechanics of a continuous medium" , Moscow (1965) (In Russian) |
| [8] | L.S. Pontryagin, "Hermitian operators in spaces with indefinite metric" Izv. Akad. Nauk SSSR Ser. Mat. , 8 (1944) pp. 243–280 (In Russian) |
| [9] | V.B. Lidskii, "On completeness of a system of eigenelements and associated functions of a nonselfadjoint operator" Dokl. Akad. Nauk. SSSR , 110 : 2 (1956) pp. 172–175 (In Russian) |
| [10] | M.S. Agranovich, "Summability of series in root vectors of non-self-adjoint elliptic operators" Funct. Anal. Appl. , 10 : 3 (1976) pp. 1–3 Funktsional. Anal. i Prilozhen. , 10 : 3 (1976) pp. 1–12 |
| [11] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , Transl. Math. Monogr. , 18 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [12] | V.E. Katsnel'son, "Conditions under which systems of eigenvectors of some classes of operators form a basis" Funct. Anal. Appl. , 1 : 2 (1967) pp. 122–133 Funksional. Anal. i Prilozhen. , 1 : 2 (1967) pp. 39–51 |
| [13] | B.V. Lidskii, "Conditions for complete continuity of the resolvent of a differential operator" Dokl. Akad. Nauk SSSR , 113 : 1 (1957) pp. 28–31 (In Russian) |
| [14] | A.G. Kostyuchenko, "Asymptotic distribution of the eigenvalues of elliptic operators" Soviet Math. Dokl. , 5 : 5 (1964) pp. 1171–1175 Dokl. Akad. Nauk. SSSR , 158 : 1 (1964) pp. 41–44 |
| [15] | S.M. Ponomarev, "A generalization of M.V. Keldysh's theorem concerning the completeness of eigen- and associated functions of the first boundary value problem for a nonself-adjoint elliptic operator" Diff. Eq. , 10 : 12 (1974) pp. 1777–1779 Differentsial. Uravnen. , 10 : 12 (1974) pp. 2294–2296 |
| [16] | N.M. Krukovskii, "The 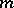 -tuple completeness of the system of generalized eigenfunctions and associated functions of a non-self-adjoint elliptic operator" Diff. Eq. , 12 : 10 (1976) pp. 1290–1296 Differentsial. Uravnen. , 12 : 10 (1976) pp. 1832–1851 -tuple completeness of the system of generalized eigenfunctions and associated functions of a non-self-adjoint elliptic operator" Diff. Eq. , 12 : 10 (1976) pp. 1290–1296 Differentsial. Uravnen. , 12 : 10 (1976) pp. 1832–1851 |
| [17] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Theory and applications of Volterra operators in Hilbert space" , Amer. Math. Soc. (1970) (Translated from Russian) |
| [18] | M.S. Brodskii, G.E. Kisilevskii, "Criterion for unicellularity of dissipative Volterra operators with nuclear imaginary components" Izv. Akad. Nauk SSSR Ser. Mat. , 30 : 6 (1966) pp. 1213–1228 (In Russian) |
| [19] | N.K. Nikol'skii, "The unicellularity and nonunicellularity of weighted shift operators" Soviet Math. Dokl. , 8 : 1 (1967) pp. 91–94 Dokl. Akad. Nauk SSSR , 172 : 2 (1967) pp. 287–290 |
| [20] | M.A. Naimark, "Investigation of the spectrum and the expansion in eigenfunctions of a second-order non-self-adjoint operator on a semi-axis" Trudy Moskov. Mat. Obshch. , 3 (1954) pp. 181–270 (In Russian) |
| [21] | M.A. Naimark, "Linear differential operators" , 1–2 , Harrap (1968) (Translated from Russian) |
| [22] | M.G. Gasymov, "Expansion in solutions of the scattering problem for a nonselfadjoint Schrödinger equation" Dokl. Akad. Nauk AzSSR , 22 : 10 (1966) pp. 9–12 (In Russian) |
| [23] | V.A. Marchenko, "Eigenfunction expansions of non-self-adjoint singular second-order differential operators" Mat. Sb. , 52 (1960) pp. 739–788 (In Russian) |
| [24] | V.A. Sadovnichii, "Analytic properties of solutions of system of equations with singularities that form segments" Trudy Sem. Petrov. , 2 (1976) pp. 211–221 (In Russian) |
| [25] | Ya.D. Tamarkin, "On some general problems of the theory of ordinary linear differential equations..." , Petrograd (1917) (In Russian) |
| [26a] | L.E. Ward, "An irregular boundary value and expansion problem" Ann. of Math. (2) , 26 (1925) pp. 21–36 |
| [26b] | L.E. Ward, "A third order irregular boundary value problem and the associated series" Trans. Amer. Math. Soc. , 34 (1932) pp. 417–434 |
| [27] | A.P. Khromov, , Proc. 2-nd Conf. Inst. Higher Education , 1 , Kuibyshev (1962) pp. 109–113 (In Russian) |
| [28] | V.P. Mikhailov, "Riesz bases in 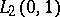 " Soviet Math. Dokl. , 3 : 3 (1962) pp. 851–854 Dokl. Akad. Nauk SSSR , 144 : 5 (1962) pp. 981–984 " Soviet Math. Dokl. , 3 : 3 (1962) pp. 851–854 Dokl. Akad. Nauk SSSR , 144 : 5 (1962) pp. 981–984 |
| [29] | G.M. Kessel'man, Izv. Vyzov. Mat. , 2 (1964) pp. 82–93 |
| [30] | V.A. Il'in, "On the properties of a reduced system of eigenfunctions and associated functions of a Keldysh bundle of ordinary differential operators" Soviet Math. Dokl. , 17 : 5 (1976) pp. 1247–1250 Dokl. Akad. Nauk SSSR , 230 (1976) pp. 30–33 |
| [31] | E.N. Moisev, "The uniform convergence of certain expansions in a closed domain" Soviet Math. Dokl. , 18 : 2 (1977) pp. 549–553 Dokl. Akad. Nauk SSSR , 233 (1977) pp. 1042–1045 |
| [32] | V.V. Tikhomirov, "On the Riesz means of expansions in eigenfunctions and associated functions of a nonselfadjoint ordinary differential operator" Math. USSR Sb. , 31 : 1 (1977) pp. 29–48 Mat. Sb. , 102 : 1 (1977) pp. 33–55 |
| [33] | V.B. Lidskii, "Fourier series expansion of principal functions of a non-self-adjoint elliptic operator" Mat. Sb. , 57 : 2 (1962) pp. 137–150 (In Russian) |
| [34] | A.A. Samarskii, Uspekhi Mat. Nauk , 5 : 3 (1950) pp. 133–134 |
| [35] | A.N. Tikhonov, "Regularization of incorrectly posed problems" Soviet Math. Dokl. , 4 : 6 (1963) pp. 1624–1627 Dokl. Akad. Nauk SSSR , 153 : 1 (1963) pp. 49–52 |
| [36] | I.M. Gel'fand, B.M. Levitan, "On a simple identity for the characteristic values of a second-order differential operator" Dokl. Akad. Nauk SSSR , 88 : 4 (1953) pp. 593–596 (In Russian) |
| [37] | V.B. Lidskii, V.A. Sadovnichii, "Regularized sums of zeros for a class of entire functions" Soviet Math. Dokl. , 8 : 5 (1967) pp. 1082–1085 Dokl. Akad. Nauk SSSR , 176 : 2 (1967) pp. 259–262 |
| [38] | V.A. Sadovnichii, "The zeta-function and eigenvalues of differential operators" Diff. Eq. , 10 : 7 (1974) pp. 986–994 Differentsial. Uravnen. , 10 : 7 (1974) pp. 1276–1285 |
| [39] | V.A. Lyubishkin, V.A. Sadovnichii, "Regularized traces of discrete operators" Soviet Math. Dokl. , 24 : 3 (1981) pp. 514–517 Dokl. Akad. Nauk SSSR , 261 : 2 (1981) pp. 290–293 |
| [40] | M.V. Keldysh, V.B. Lidskii, "On the spectral theory of nonselfadjoint operators" , Fourth All-Union Math. Congress , 1 , Leningrad (1963) pp. 101–120 (In Russian) |
| [41] | P.D. Lax, R.S. Philipps, "Scattering theory for automorphic functions" , Princeton Univ. Press (1976) |
| [42] | B. Szökefalvi-Nagy, Ch. Foiaş, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) (Translated from French) |
| [43] | V.P. Maslov, "Operational methods" , MIR (1976) (Translated from Russian) |
| [44] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral operators" , 3 , Interscience (1971) |
Comments
The main article above gives a partial picture of the theory of non-self-adjoint operators. The method of Keldysh about multiple completeness is explained in detail. A second important method, which has been developed by M.G. Krein and H. Langer (see [7]), is only touched upon. The Krein–Langer method uses factorization as a tool.
Consider the quadratic operator polynomial 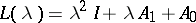 , where
, where 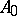 and
and 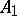 are bounded linear operators acting on a Hilbert space
are bounded linear operators acting on a Hilbert space 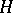 , and let
, and let 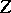 be a (right) operator root of
be a (right) operator root of 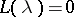 , that is,
, that is,
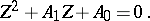 |
Then 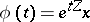 is a solution of the differential equation
is a solution of the differential equation 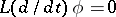 for each
for each 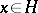 . One of the problems is to find operator roots
. One of the problems is to find operator roots 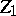 and
and 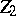 of
of 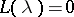 so that
so that
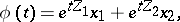 |
where  and
and 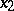 run over all vectors in
run over all vectors in 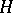 , form the set of all solutions of
, form the set of all solutions of 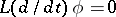 . Moreover, if such
. Moreover, if such 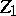 and
and 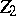 have been found, one would like to know when the linear span of elementary solutions of the equations
have been found, one would like to know when the linear span of elementary solutions of the equations
 |
is dense (in a sense to be made more precise) in the space of all solutions. If 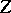 is an operator root, then
is an operator root, then 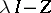 is a right divisor of
is a right divisor of 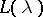 , that is,
, that is,
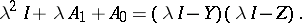 | (a1) |
The method of Krein–Langer uses the theory of spaces with an indefinite metric (cf. Space with an indefinite metric) to obtain factorizations of the type (a1) and to analyze their properties for the important case when 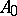 and
and 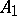 are self-adjoint. Here indefinite metrics turn up naturally, because the companion operator
are self-adjoint. Here indefinite metrics turn up naturally, because the companion operator
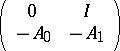 |
is self-adjoint relative to the indefinite metric
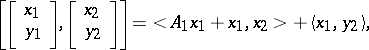 |
whenever 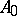 and
and 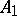 are self-adjoint relative to the usual product
are self-adjoint relative to the usual product 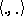 on
on 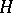 . The Krein–Langer method is, therefore, of a geometric nature, while Keldysh's method has an analytic character.
. The Krein–Langer method is, therefore, of a geometric nature, while Keldysh's method has an analytic character.
The Krein–Langer approach has led to two directions of research. One continued to use and develop further the geometric methods of operator theory in spaces with an indefinite metric, with Langer as one of the main contributors. The other direction adapted Wiener–Hopf factorization methods for operator-valued functions and used these analytical tools to study the spectral properties of polynomials and analytic operator functions. Here the main contributors are A.S. Markus and V.I. Matsaev. The Keldysh method and the Krein–Langer method are nicely presented in [a1]. Parallel, but with a stronger emphasis on the finite-dimensional case, the factorization direction was also developed in the Western literature. In the latter, connections with mathematical systems theory played an important role (see, e.g., [a2]–[a4]).
A third major method in the theory of non-self-adjoint operators, probably the oldest in this area, was initiated in the middle of the 1940s by M.S. Lifshits. The main tool here is the characteristic operator function, which is associated with an arbitrary operator 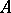 in the following way:
in the following way:
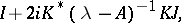 |
where 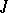 is a signature operator (i.e.
is a signature operator (i.e. 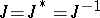 ) and
) and 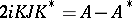 . This function serves as a unitary invariant for the operator
. This function serves as a unitary invariant for the operator 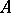 (some trivial self-adjoint parts excluded), and in several important cases it is much easier to analyze than the original operator. The characteristic operator function has intriguing properties, for example, from its divisors invariant subspaces of the operator
(some trivial self-adjoint parts excluded), and in several important cases it is much easier to analyze than the original operator. The characteristic operator function has intriguing properties, for example, from its divisors invariant subspaces of the operator 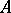 may be read off. The theory of characteristic operator functions has been extended in many different directions by M.S. Brodskii, L.A. Sakhnovich, I.C. Gohberg and Krein (see [a5], [a6], [11], [17]). A far-reaching development connected with the theory of characteristic operator functions concerns the study of contractive operators by B. Sz.-Nagy and C. Foiaş [42], which has led to a complete understanding of a wide class of non-self-adjoint operators [a7].
may be read off. The theory of characteristic operator functions has been extended in many different directions by M.S. Brodskii, L.A. Sakhnovich, I.C. Gohberg and Krein (see [a5], [a6], [11], [17]). A far-reaching development connected with the theory of characteristic operator functions concerns the study of contractive operators by B. Sz.-Nagy and C. Foiaş [42], which has led to a complete understanding of a wide class of non-self-adjoint operators [a7].
Another original method in the theory of non-self-adjoint operators is due to L. de Branges and his co-workers ([a8], [a9]). The method of de Branges is based on a deep analysis of the theory of spaces of entire vector-valued functions. Here the mapping
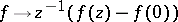 |
provides the main model. Recently this approach led to a sensational success by yielding a proof of the Bieberbach conjecture [a10].
References
| [a1] | A.S. Markus, "Introduction to the spectral theory of polynomial operator pencils" , Amer. Math. Soc. (1986) (Translated from Russian) |
| [a2] | I. Gohberg, P. Lancaster, L. Rodman, "Matrix polynomials" , Acad. Press (1982) |
| [a3] | H. Bart, I. Gohberg, M.A. Kaashoek, "Minimal factorization of matrix and operation functions" , Birkhäuser (1979) |
| [a4] | L. Rodman, "An introduction to operator polynomials" , Birkhäuser (1989) |
| [a5] | M.S. [M.S. Lifshits] Livšic, "Operators, oscillations, waves" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [a6] | M.S. Brodskii, "Triangular and Jordan representations of linear operators" , Amer. Math. Soc. (1971) (Translated from Russian) |
| [a7] | H. Bercovici, "Operator theory and arithmetic in 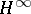 " , Amer. Math. Soc. (1988) " , Amer. Math. Soc. (1988) |
| [a8] | L. de Branges, "Hilbert spaces of entire functions" , Prentice-Hall (1968) |
| [a9] | L. de Branges, J. Rovnyak, "Square summable power series" , Rinehart & Winston (1966) |
| [a10] | L. de Branges, "A proof of the Bieberbach conjecture" Acta Math. , 154 (1985) pp. 137–152 |
| [a11] | M.S. Brodskii, M.S. [M.S. Lifshits] Livšic, "Spectral analysis of non-selfadjoint operators and intermediate systems" Transl. Amer. Math. Soc. (2) , 13 (1960) pp. 265–346 |
| [a12] | H.R. Dowson, "Spectral theory of linear operators" , Acad. Press (1978) |
Non-self-adjoint operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-self-adjoint_operator&oldid=14752