Non-cooperative game
A system
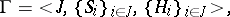 |
where  is the set of players,
is the set of players,  is the set of strategies (cf. Strategy (in game theory)) of the
is the set of strategies (cf. Strategy (in game theory)) of the  -th player and
-th player and  is the gain function of the
is the gain function of the  -th player, defined on the Cartesian product
-th player, defined on the Cartesian product  . A non-cooperative game is played as follows: players, who are acting individually (do not form a coalition, do not cooperate), select their strategies
. A non-cooperative game is played as follows: players, who are acting individually (do not form a coalition, do not cooperate), select their strategies  , as a result of which the situation
, as a result of which the situation 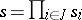 appears, in which the
appears, in which the 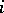 -th player obtains the gain
-th player obtains the gain 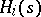 . The main optimality principle in a non-cooperative game is the principle of realizability of the objective [1], which generates the Nash equilibrium solutions. A solution
. The main optimality principle in a non-cooperative game is the principle of realizability of the objective [1], which generates the Nash equilibrium solutions. A solution 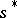 is called an equilibrium solution if for all
is called an equilibrium solution if for all 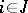 ,
, 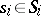 , the inequality
, the inequality
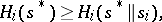 |
where  , is valid. Thus, none of the players is interested in unilaterally disturbing the equilibrium solution previously agreed upon between them. It has been proved (Nash's theorem) that a finite non-cooperative game (the sets
, is valid. Thus, none of the players is interested in unilaterally disturbing the equilibrium solution previously agreed upon between them. It has been proved (Nash's theorem) that a finite non-cooperative game (the sets 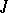 and
and 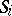 are finite) possesses an equilibrium solution for mixed strategies. This theorem has been generalized to include infinite non-cooperative games with a finite number of players [3] and non-cooperative games with an infinite number of players (cf. Non-atomic game).
are finite) possesses an equilibrium solution for mixed strategies. This theorem has been generalized to include infinite non-cooperative games with a finite number of players [3] and non-cooperative games with an infinite number of players (cf. Non-atomic game).
Two equilibrium solutions  and
and 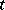 are called interchangeable if any solution
are called interchangeable if any solution 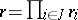 , where
, where 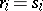 or
or 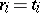 ,
, 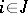 , is also an equilibrium solution. They are called equivalent if
, is also an equilibrium solution. They are called equivalent if 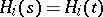 for all
for all 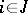 . Let
. Let 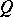 be the set of all equilibrium solutions, and let
be the set of all equilibrium solutions, and let 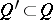 be the set of equilibrium solutions which are Pareto optimal (cf. Arbitration scheme). A game is called Nash solvable and
be the set of equilibrium solutions which are Pareto optimal (cf. Arbitration scheme). A game is called Nash solvable and 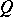 is said to be a Nash solution if all
is said to be a Nash solution if all 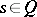 are equivalent and interchangeable. A game is called strictly solvable if
are equivalent and interchangeable. A game is called strictly solvable if 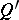 is non-empty and all
is non-empty and all 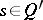 are equivalent and interchangeable. Two-person zero-sum games (cf. Two-person zero-sum game) with optimal strategies are Nash solvable and strictly solvable; however, in the general case such a solvability is often impossible.
are equivalent and interchangeable. Two-person zero-sum games (cf. Two-person zero-sum game) with optimal strategies are Nash solvable and strictly solvable; however, in the general case such a solvability is often impossible.
Other attempts at completing the principle of realizability of the objective were made. Thus, it was suggested [4] that the unique equilibrium solution or the maximum solution (in this last situation each player may ensure his/her own gain irrespective of the strategies chosen by the other players), the choice of which is based on the introduction of a new preference relation on the set of solutions, be considered as the solution of the non-cooperative game. In another approach the solution of a non-cooperative game is defined by a subjective prognosis of the behaviour of the players [5].
References
| [1] | N.N. Vorob'ev, "The present state of the theory of games" Russian Math. Surveys , 25 : 2 (1970) pp. 77–136 Uspekhi Mat. Nauk , 25 : 2 (1970) pp. 81–140 |
| [2] | J. Nash, "Noncooperative games" Ann. of Math. , 54 (1951) pp. 286–295 |
| [3] | I.L. Glicksberg, "A further generalization of the Kakutani fixed point theorem, with application to Nash equilibrium points" Proc. Amer. Math. Soc. , 3 (1952) pp. 170–174 |
| [4] | J.C. Harsanyi, "A general solution for finite noncooperative games based on risk-dominance" L.S. Shapley (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Advances in game theory , Princeton Univ. Press (1964) pp. 651–679 |
| [5] | E.I. Vilkas, "The axiomatic definition of equilibrium points and the value of a non-coalition  -person game" Theory Probab. Appl. , 13 : 3 (1968) pp. 523–527 Teor. Veroyatnost. i Primenen. , 13 : 3 (1968) pp. 555–560 -person game" Theory Probab. Appl. , 13 : 3 (1968) pp. 523–527 Teor. Veroyatnost. i Primenen. , 13 : 3 (1968) pp. 555–560 |
Comments
References
| [a1] | N.N. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian) |
Non-cooperative game. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-cooperative_game&oldid=17485