Noetherian ring
left (right)
A ring  satisfying one of the following equivalent conditions:
satisfying one of the following equivalent conditions:
1)  is a left (or right) Noetherian module over itself;
is a left (or right) Noetherian module over itself;
2) every left (or right) ideal in  has a finite generating set;
has a finite generating set;
3) every strictly ascending chain of left (or right) ideals in  breaks off after finitely many terms.
breaks off after finitely many terms.
An example of a Noetherian ring is any principal ideal ring, i.e. a ring in which every ideal has one generator.
Noetherian rings are named after E. Noether, who made a systematic study of such rings and carried over to them a number of results known earlier only under more stringent restrictions (for example, Lasker's theory of primary decompositions).
A right Noetherian ring need not be left Noetherian and vice versa. For example, let  be the ring of matrices of the form
be the ring of matrices of the form
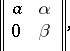 |
where  is a rational integer and
is a rational integer and  and
and  are rational numbers, with the usual addition and multiplication. Then
are rational numbers, with the usual addition and multiplication. Then 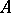 is right, but not left, Noetherian, since the left ideal of elements of the form
is right, but not left, Noetherian, since the left ideal of elements of the form
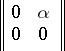 |
does not have a finite generating set.
Quotient rings and finite direct sums of Noetherian rings are again Noetherian, but a subring of a Noetherian ring need not be Noetherian. For example, a polynomial ring in infinitely many variables over a field is not Noetherian, although it is contained in its field of fractions, which is Noetherian.
If  is a left Noetherian ring, then so is the polynomial ring
is a left Noetherian ring, then so is the polynomial ring  . The corresponding property holds for the ring of formal power series over a Noetherian ring. In particular, polynomial rings of the form
. The corresponding property holds for the ring of formal power series over a Noetherian ring. In particular, polynomial rings of the form 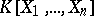 or
or  , where
, where  is a field and
is a field and  the ring of integers, and also quotient rings of them, are Noetherian. Every Artinian ring is Noetherian. The localization of a commutative Noetherian ring
the ring of integers, and also quotient rings of them, are Noetherian. Every Artinian ring is Noetherian. The localization of a commutative Noetherian ring  relative to some multiplicative system
relative to some multiplicative system  is again Noetherian. If in a commutative Noetherian ring
is again Noetherian. If in a commutative Noetherian ring 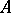 ,
, 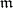 is an ideal such that no element of the form
is an ideal such that no element of the form 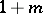 , where
, where 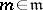 , is a divisor of zero, then
, is a divisor of zero, then  . This means that any such ideal
. This means that any such ideal 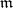 defines on
defines on 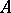 a separable
a separable  -adic topology. In a commutative Noetherian ring every ideal has a representation as an incontractible intersection of finitely many primary ideals. Although such a representation is not unique, the number of ideals and the set of prime ideals associated with the given primary ideals are uniquely determined.
-adic topology. In a commutative Noetherian ring every ideal has a representation as an incontractible intersection of finitely many primary ideals. Although such a representation is not unique, the number of ideals and the set of prime ideals associated with the given primary ideals are uniquely determined.
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [3] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) |
Noetherian ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Noetherian_ring&oldid=18864