Noetherian module
From Encyclopedia of Mathematics
A module for which every submodule has a finite system of generators. Equivalent conditions are: Every strictly ascending chain of submodules breaks off after finitely many terms; every non-empty set of submodules ordered by inclusion contains a maximal element. Submodules and quotient modules of a Noetherian module are Noetherian. If, in an exact sequence
 |
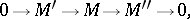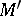and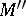 
are Noetherian, then so is 
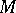. A module over a Noetherian ring is Noetherian if and only if it is finitely generated.
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1974) |
How to Cite This Entry:
Noetherian module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Noetherian_module&oldid=13634
Noetherian module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Noetherian_module&oldid=13634
This article was adapted from an original article by L.V. Kuz'min (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article