Node
A point of self-intersection of a curve. For a parametrically given curve a node corresponds to two or more values of the parameter. E.g. for the curve 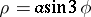 the origin of coordinates is a node.
the origin of coordinates is a node.

Figure: n066760a
Comments
A reference for "node of a curve" is [a1].
References
| [a1] | J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) |
A node is a type of arrangement of the trajectories of an autonomous system of second-order ordinary differential equations
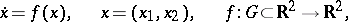 | (*) |
 ,
, 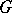 a domain of uniqueness, in a neighbourhood of a stationary point
a domain of uniqueness, in a neighbourhood of a stationary point 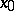 . This type is characterized in the following way. There exists a neighbourhood
. This type is characterized in the following way. There exists a neighbourhood  of
of  such that for all trajectories of the system beginning in
such that for all trajectories of the system beginning in  the negative semi-trajectories leave in the course of time any compact set
the negative semi-trajectories leave in the course of time any compact set 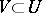 , while the positive semi-trajectories approach
, while the positive semi-trajectories approach 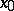 while not leaving
while not leaving 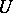 and, moreover, being completed with
and, moreover, being completed with 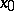 , touch it in well-defined directions, or vice versa. The point
, touch it in well-defined directions, or vice versa. The point 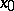 itself is also called a node, a nodal point or a basis point.
itself is also called a node, a nodal point or a basis point.
A node is either asymptotically stable in the sense of Lyapunov (cf. Lyapunov stability) or is totally unstable (asymptotically stable for 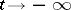 ). The Poincaré index of a node is 1 (cf. Singular point).
). The Poincaré index of a node is 1 (cf. Singular point).
For a system (*) of class 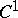 (
(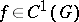 ) with non-zero matrix
) with non-zero matrix  , a stationary point
, a stationary point 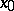 is a node if the eigen values
is a node if the eigen values 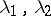 of
of 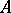 are real and satisfy the conditions
are real and satisfy the conditions 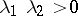 ,
, 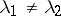 ; it can also be a node in cases when
; it can also be a node in cases when 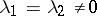 ,
, 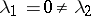 ,
, 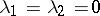 . In case
. In case 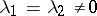 ,
,  will be a node if
will be a node if 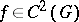 ; when this condition is not satisfied it may turn out to be focus. In any of the cases listed above the trajectories of the system converging to the node
; when this condition is not satisfied it may turn out to be focus. In any of the cases listed above the trajectories of the system converging to the node 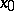 touch it in well-defined directions, defined by the eigen vectors of
touch it in well-defined directions, defined by the eigen vectors of 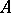 . If
. If 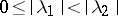 , there exist four such directions (if diametrically opposite ones are counted as distinct), and two trajectories of the system touch at
, there exist four such directions (if diametrically opposite ones are counted as distinct), and two trajectories of the system touch at 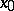 in directions corresponding to the eigen value
in directions corresponding to the eigen value  while two trajectories touch at
while two trajectories touch at 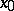 in directions corresponding to the eigen value
in directions corresponding to the eigen value 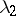 (Fig. a). These are ordinary nodes. If
(Fig. a). These are ordinary nodes. If 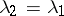 , then the eigen directions for
, then the eigen directions for 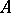 at
at  are either just two opposite directions (in this case the node is degenerate, cf. Fig. b) or all directions. In this last case, under the condition
are either just two opposite directions (in this case the node is degenerate, cf. Fig. b) or all directions. In this last case, under the condition 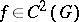 every direction is tangent at
every direction is tangent at 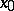 to a unique trajectory of the system. Such a node is called dicritical (Fig. c). VOL 5 COL 475 !
to a unique trajectory of the system. Such a node is called dicritical (Fig. c). VOL 5 COL 475 !
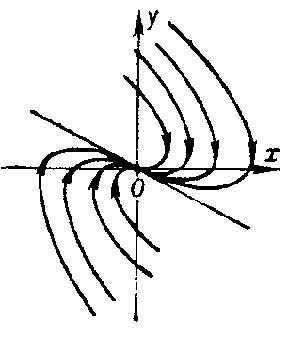
Figure: n066760b
VOL 5 COL 475 !
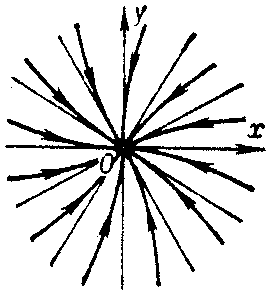
Figure: n066760c
VOL 5 COL 475 !
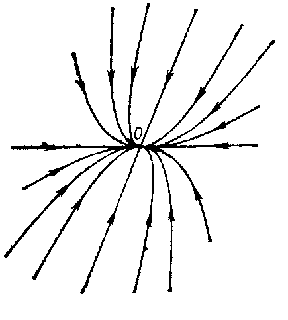
Figure: n066760d
If the system (*) is linear (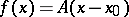 , where
, where 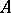 is a fixed matrix) then the point
is a fixed matrix) then the point 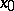 is a node only when the eigen values
is a node only when the eigen values 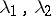 of
of 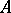 are real and
are real and  . Any ray
. Any ray 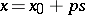 (
( an eigen vector of
an eigen vector of 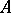 ,
, 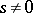 a parameter) is a trajectory for it. Ordinary, degenerate and dicritical nodes for a linear system are depicted in Fig. d, Fig. eand Fig. f.
a parameter) is a trajectory for it. Ordinary, degenerate and dicritical nodes for a linear system are depicted in Fig. d, Fig. eand Fig. f.

Figure: n066760e

Figure: n066760f

Figure: n066760g
In the case of an ordinary node all curvilinear trajectories are affine images of parabolas 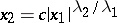 ,
, 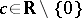 .
.
The term "node" is also applied to a stationary point of a system of the form (*) of order 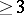 with analogous behaviour of the trajectories in neighbourhoods of it.
with analogous behaviour of the trajectories in neighbourhoods of it.
For references see Singular point of a differential equation.
Comments
References
| [a1] | S. Lefshetz, "Differential equations: geometric theory" , Dover, reprint (1977) pp. Sect. IX.2 |
| [a2] | G. Birkhoff, G.-C. Rota, "Ordinary differential equations" , Ginn (1962) pp. Sect. VI.8 |
Node. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Node&oldid=12598