Nilpotent semi-group
A semi-group 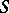 with zero for which there is an
with zero for which there is an  such that
such that 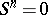 ; this is equivalent to the identity
; this is equivalent to the identity
 |
in 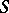 . The smallest
. The smallest  with this property for a given semi-group is called the step (sometimes class) of nilpotency. If
with this property for a given semi-group is called the step (sometimes class) of nilpotency. If 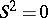 , then
, then 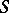 is called a semi-group with zero multiplication. The following conditions on a semi-group
is called a semi-group with zero multiplication. The following conditions on a semi-group 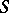 are equivalent: 1)
are equivalent: 1) 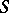 is nilpotent; 2)
is nilpotent; 2) 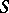 has a finite annihilator series (that is, an ascending annihilator series of finite length, see Nil semi-group); or 3) there is a
has a finite annihilator series (that is, an ascending annihilator series of finite length, see Nil semi-group); or 3) there is a 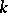 such that every sub-semi-group of
such that every sub-semi-group of  can be imbedded as an ideal series of length
can be imbedded as an ideal series of length 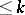 .
.
A wider concept is that of a nilpotent semi-group in the sense of Mal'tsev [2]. This is the name for a semi-group satisfying for some  the identity
the identity
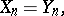 |
where the words 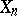 and
and 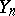 are defined inductively as follows:
are defined inductively as follows: 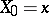 ,
, 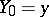 ,
, 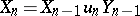 ,
,  , where
, where  ,
,  and
and  are variables. A group is a nilpotent semi-group in the sense of Mal'tsev if and only if it is nilpotent in the usual group-theoretical sense (see Nilpotent group), and the identity
are variables. A group is a nilpotent semi-group in the sense of Mal'tsev if and only if it is nilpotent in the usual group-theoretical sense (see Nilpotent group), and the identity 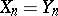 is equivalent to the fact that its class of nilpotency is
is equivalent to the fact that its class of nilpotency is 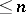 . Every cancellation semi-group satisfying the identity
. Every cancellation semi-group satisfying the identity 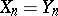 can be imbedded in a group satisfying the same identity.
can be imbedded in a group satisfying the same identity.
References
| [1] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [2] | A.I. Mal'tsev, "Nilpotent semi-groups" Uchen. Zap. Ivanov. Gos. Ped. Inst. , 4 (1953) pp. 107–111 (In Russian) |
| [3] | L.N. Shevrin, "On the general theory of semi-groups" Mat. Sb. , 53 : 3 (1961) pp. 367–386 (In Russian) |
| [4] | L.N. Shevrin, "Semi-groups all sub-semi-groups of which are accessible" Mat. Sb. , 61 : 2 (1963) pp. 253–256 (In Russian) |
Nilpotent semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nilpotent_semi-group&oldid=13014