Nil semi-group
A semi-group with zero in which some power of every element is zero. Nil semi-groups form one of the most important classes of periodic semi-groups (cf. Periodic semi-group): They are precisely the periodic semi-groups with a unique idempotent, namely, the zero. Locally nilpotent semi-groups (that is, semi-groups in which every finitely-generated sub-semi-group is nilpotent, see Nilpotent semi-group) form a narrow class. For every  , there exists a semi-group with the identity
, there exists a semi-group with the identity  that is not locally nilpotent (see, for example, [1], Chapt. 8 Sect. 4). A finite nil semi-group is nilpotent, and the classes of locally nilpotent semi-groups and locally finite nil semi-groups coincide (see Locally finite semi-group). An even narrower class is formed by the semi-groups with an ascending annihilator series. A semi-group
that is not locally nilpotent (see, for example, [1], Chapt. 8 Sect. 4). A finite nil semi-group is nilpotent, and the classes of locally nilpotent semi-groups and locally finite nil semi-groups coincide (see Locally finite semi-group). An even narrower class is formed by the semi-groups with an ascending annihilator series. A semi-group 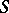 has an ascending annihilator series if it has an increasing ideal series (see Ideal series of a semi-group) such that for any two adjacent terms
has an ascending annihilator series if it has an increasing ideal series (see Ideal series of a semi-group) such that for any two adjacent terms 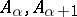 ,
,
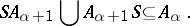 |
A nil semi-group has an ascending annihilator series if and only if it has an increasing series of ideals in which all factors are finite. Every semi-group with an ascending annihilator series has a unique irreducible generating set, consisting of its indecomposable elements. An arbitrary locally nilpotent semi-group may coincide with its square. Many finiteness conditions (see Semi-group with a finiteness condition) imposed on a semi-group imply that is finite; for example, the minimum condition for ideals, or the maximum condition for right (or left) ideals. If all nilpotent sub-semi-groups of a nil semi-group  are finite, then so is
are finite, then so is 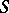 .
.
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
| [2] | L.N. Shevrin, "On the general theory of semi-groups" Mat. Sb. , 53 : 3 (1961) pp. 367–386 (In Russian) |
| [3] | L.N. Shevrin, "Nil semi-groups with certain finiteness conditions" Mat. Sb. , 55 : 4 (1961) pp. 473–480 (In Russian) |
Nil semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nil_semi-group&oldid=14044