Nikodým boundedness theorem
A theorem [a5], [a4], saying that a family  of countably additive signed measures
of countably additive signed measures  (cf. Measure) defined on a
(cf. Measure) defined on a  -algebra
-algebra  and pointwise bounded, i.e. for each
and pointwise bounded, i.e. for each 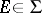 there exists a number
there exists a number  such that
such that
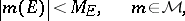 |
is uniformly bounded, i.e. there exists a number  such that
such that
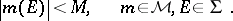 |
As is well-known, the Nikodým boundedness theorem for measures fails in general for algebras of sets. But there are uniform boundedness theorems in which the initial boundedness conditions are imposed on certain subfamilies of a given 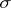 -algebra; those subfamilies need not be
-algebra; those subfamilies need not be 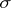 -algebras. The following definitions are useful [a2], [a7], [a8]:
-algebras. The following definitions are useful [a2], [a7], [a8]:
SCP) An algebra 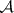 has the sequential completeness property if each disjoint sequence
has the sequential completeness property if each disjoint sequence 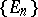 from
from 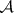 has a subsequence
has a subsequence 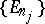 whose union is in
whose union is in 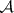
SIP) An algebra 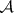 has the subsequential interpolation property if for each subsequence
has the subsequential interpolation property if for each subsequence 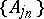 of each disjoint sequence
of each disjoint sequence 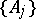 from
from 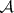 there are a subsequence
there are a subsequence 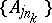 and a set
and a set 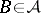 such that
such that
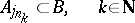 |
and 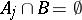 for
for 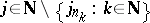 .
.
The Nikodým boundedness theorem holds on algebras with SCP) and SIP).
A famous theorem of J. Dieudonné [a3] states that for compact metric spaces the pointwise boundedness of a family of regular Borel measures on open sets implies its uniform boundedness on all Borel sets. There are further generalizations of this theorem [a6].
See also Nikodým convergence theorem; Diagonal theorem.
References
| [a1] | P. Antosik, C. Swartz, "Matrix methods in analysis" , Lecture Notes Math. , 1113 , Springer (1985) |
| [a2] | C. Constantinescu, "On Nikodym's boundedness theorem" Libertas Math. , 1 (1981) pp. 51–73 |
| [a3] | J. Dieudonné, "Sur la convergence des suites de mesures de Radon" An. Acad. Brasil. Ci. , 23 (1951) pp. 21–38, 277–282 |
| [a4] | N. Dunford, J.T. Schwartz, "Linear operators Part I" , Interscience (1958) |
| [a5] | O. Nikodym, "Sur les familles bornées de functions parfaitement additives d'ensembles abstraits" Monatsh. Math. , 40 (1933) pp. 418–426 |
| [a6] | E. Pap, "Null-additive set functions" , Kluwer Acad. Publ. &Ister Sci. (1995) |
| [a7] | W. Schachermayer, "On some classsical measure-theoretic theorems for non-sigma complete Boolean algebras" Dissert. Math. , 214 (1982) pp. 1–33 |
| [a8] | H. Weber, "Compactness in spaces of group-valued contents, the Vitali–Hahn–Saks theorem and the Nikodym's boundedness theorem" Rocky Mtn. J. Math. , 16 (1986) pp. 253–275 |
Nikodým boundedness theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nikod%C3%BDm_boundedness_theorem&oldid=15213