Nicomedes conchoid
From Encyclopedia of Mathematics
A plane algebraic curve of order 4 whose equation in Cartesian rectangular coordinates has the form
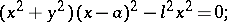 |
and in polar coordinates
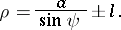 |
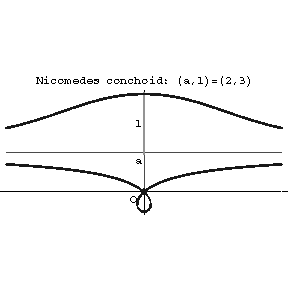
Figure: n066620a
Outer branch (see Fig.). Asymptote  . Two points of inflection,
. Two points of inflection, 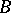 and
and 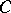 .
.
Inner branch. Asymptote  . The coordinate origin is a double point whose character depends on the values of
. The coordinate origin is a double point whose character depends on the values of  and
and 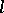 . For
. For 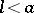 it is an isolated point and, in addition, the curve has two points of inflection,
it is an isolated point and, in addition, the curve has two points of inflection, 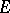 and
and 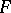 ; for
; for 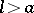 it is a node; for
it is a node; for 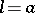 it is a cusp. The curve is a conchoid of the straight line
it is a cusp. The curve is a conchoid of the straight line  .
.
The curve is named after Nicomedes (3rd century B.C.), who used it to solve the problem of trisecting an angle.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
How to Cite This Entry:
Nicomedes conchoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nicomedes_conchoid&oldid=13493
Nicomedes conchoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nicomedes_conchoid&oldid=13493
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article