Newton diagram
Newton polygon
A convex polygonal line, introduced by I. Newton in 1669 (see [1]) to determine the exponents of the principal terms of algebraic functions. The process of finding successively the terms of the expansion of an algebraic function with the help of the Newton diagram is called the method of the Newton diagram. In more detail it was worked out by V. Puiseux [2] and it is sometimes called the Puiseux diagram in mathematical literature. Before Puiseux, an algebraic version of the Newton diagram was studied by J.L. Lagrange [3].
Let 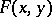 be a pseudo-polynomial in
be a pseudo-polynomial in 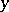 , that is, let
, that is, let
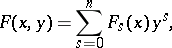 |
where
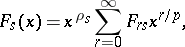 |
 and
and 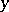 are complex variables,
are complex variables, 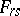 are complex numbers,
are complex numbers, 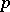 is a natural number,
is a natural number, 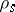 are non-negative rational numbers,
are non-negative rational numbers, 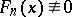 , and
, and 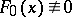 . As a rule one assumes that if
. As a rule one assumes that if 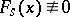 , then
, then  , hence,
, hence, 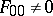 ,
, 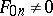 . A solution
. A solution 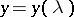 of the equation
of the equation
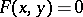 | (1) |
is sought for in the form of a series
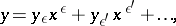 | (2) |
where  or, briefly,
or, briefly, 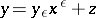 ,
, 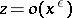 as
as  . To determine the possible values of
. To determine the possible values of  and
and 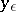 one substitutes (2) in (1), collects terms with equal powers of
one substitutes (2) in (1), collects terms with equal powers of  , and equates to zero the coefficients of these powers.
, and equates to zero the coefficients of these powers.
The process begins with the term of lowest degree. As long as the exponent  is not yet determined, there is no way of telling which of the resulting terms are lowest in
is not yet determined, there is no way of telling which of the resulting terms are lowest in  . However, the terms of lowest order are among the following:
. However, the terms of lowest order are among the following:
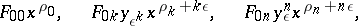 | (3) |
where 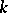 ranges over those values
ranges over those values 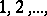 for which
for which 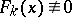 . To annihilate the terms of lowest order one has to choose
. To annihilate the terms of lowest order one has to choose  so that at least two of the exponents
so that at least two of the exponents 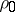 ,
, 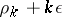 ,
, 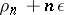 coincide and the remaining ones are to be not smaller. This argument leads to Newton's diagram.
coincide and the remaining ones are to be not smaller. This argument leads to Newton's diagram.
In the plane one takes a rectangular Cartesian coordinate system and plots the points 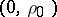 ,
, 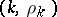 and
and 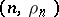 , where
, where  ranges over the same values as in (3). Through the point
ranges over the same values as in (3). Through the point 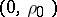 one draws the line that coincides with the
one draws the line that coincides with the 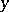 -axis and then rotates around
-axis and then rotates around  anti-clockwise until it falls onto one of the plotted points, say
anti-clockwise until it falls onto one of the plotted points, say 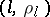 . The tangent of the angle that the line
. The tangent of the angle that the line 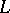 passing through
passing through 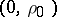 and
and 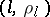 makes with the negative
makes with the negative  -axis is one of the values
-axis is one of the values  , since
, since 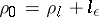 , and
, and  if
if  . Suppose that
. Suppose that 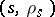 is the point on
is the point on 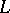 with largest
with largest  -coordinate and that
-coordinate and that 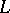 is rotated anti-clockwise around
is rotated anti-clockwise around  until it falls onto another one of the plotted points, say,
until it falls onto another one of the plotted points, say,  with
with 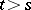 . Let
. Let 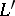 be the line through
be the line through 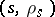 and
and  . The tangent of the angle between
. The tangent of the angle between  and the negative
and the negative  -axis gives another possible value of
-axis gives another possible value of  . Continuing these constructions one obtains a convex polygonal line, which is called Newton's diagram.
. Continuing these constructions one obtains a convex polygonal line, which is called Newton's diagram.
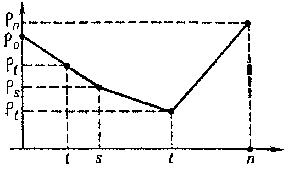
Figure: n066520a
The value of the coefficient of 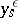 is determined as follows. Let
is determined as follows. Let 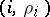 and
and 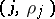 be the extreme points of a segment of the Newton diagram that determines one of the possible values of
be the extreme points of a segment of the Newton diagram that determines one of the possible values of  . To annihilate the terms of lowest order when (2) is substituted in (1) it is necessary and sufficient that
. To annihilate the terms of lowest order when (2) is substituted in (1) it is necessary and sufficient that
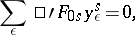 | (4) |
where the prime in the sum denotes that summation is over those  for which
for which 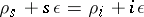 . Equation (4) has
. Equation (4) has 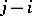 non-zero roots (including multiplicity), that is, as many as the length of the projection of the relevant segment of the Newton diagram. Hence it is clear that by the method of the Newton diagram one obtains all
non-zero roots (including multiplicity), that is, as many as the length of the projection of the relevant segment of the Newton diagram. Hence it is clear that by the method of the Newton diagram one obtains all  values of the principal term
values of the principal term 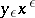 in (2). By the same method one determines the next term in the expansion (2), etc. As a result, all
in (2). By the same method one determines the next term in the expansion (2), etc. As a result, all  solutions of (1) have the form (2), so-called Puiseux series (see Algebraic function). The method of the Newton diagram is also applicable to the solution of differential equations.
solutions of (1) have the form (2), so-called Puiseux series (see Algebraic function). The method of the Newton diagram is also applicable to the solution of differential equations.
References
| [1] | I. Newton, "The mathematical papers of I. Newton" , 1–8 , Cambridge Univ. Press (1967–1981) |
| [2] | V. Puiseux, "Récherches sur les fonctions algébriques" J. Math. Pure Appl. , 15 (1850) pp. 365–480 |
| [3] | J.L. Lagrange, "Solution de quelques problèmes d'astronomie sphérique par le moyen des séries" Nouv. Mém. Acad. Roy. Sci. Belles Lettres Berlin (1776) |
| [4] | M.M. Vainberg, V.A. Trenogin, "Theory of branching of solutions of non-linear equations" , Noordhoff (1974) (Translated from Russian) |
| [5] | , Isaac Newton 1643 - 1727; a collection of articles on the tercentenary of his birth , Moscow (1943) (In Russian) |
| [6] | A.D. [A.D. Bryuno] Bruno, "Local methods in nonlinear differential equations" , Springer (1989) (Translated from Russian) |
Newton diagram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Newton_diagram&oldid=12732